Resolvi um exercício e gostaria de saber se está certo.
"Mostre que
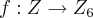 ,
,  é um homomorfismo de grupos."
é um homomorfismo de grupos."Minha resolução:
Temos que:
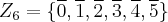 . Observemos que os grupos com os quais estamos trabalhando são
. Observemos que os grupos com os quais estamos trabalhando são  e
e 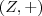 . Vamos mostrar que é homomorfismo. Segue:
. Vamos mostrar que é homomorfismo. Segue:  ;
; 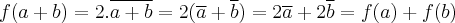 . Conseguimos, assim, mostrar que
. Conseguimos, assim, mostrar que 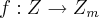 é homomorfismo. Por outro lado, basta observarmos que
é homomorfismo. Por outro lado, basta observarmos que  pode ser escrito como elemento de
pode ser escrito como elemento de 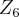 . Por exemplo:
. Por exemplo:  . Logo,
. Logo, 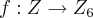 é homomorfismo.
é homomorfismo.Está certo? Muito obrigada pela ajuda!


 ,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...
,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...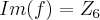 . Está certo?
. Está certo?
 .
.



