Você entendeu errado. O domínio da função é, certamente, o conjunto Real dado que
rcpn escreveu:para quaisquer números reais positivos u e v
O que o enunciado quer dizer com

é a função calculada para o produto de

e

. Por exemplo, se
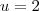
e
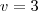
, então você calculará com esses valores
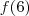
. Esta função possui uma propriedade interessante. Se você aplicar esta função em um produto a resposta(ou imagem) será a soma da aplicação dessa função em

e

separadamente. Você não conhece nenhuma função com essa propriedade? Ela é famosa!! Não há no mundo estudante de Matemática que não já tenha trabalhado com ela.
Mas, mesmo que você não lembre que função é, não é necessário conhecê-la explicitamente para resolver o exercício. O dado é que
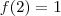
. Este é o ponto de partida. Para calcular as aplicações da função em outros números teremos de manipular este resultado.
A aplicação

é, claramente, calculável. Note que, da propriedade,

. Assim, rapidamente,
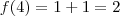
.
A aplicação
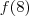
decorre, imediatamente, do resultado anterior. Podemos tomar
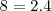
e teremos
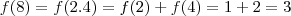
.
A aplicação

não parece, a princípio, trivial. Mas, na realidade, é a mais trivial de todas. Note que

. Daí,
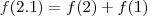
de onde

. ( A essa altura já percebemos que as aplicações capturam numéros conhecido, não?)
A próxima aplicação nos desafia um pouco mais. Precisamos manipular os resultado que já temos para calcular
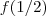
, que não aprece ser trivial. De fato, não é. Façamos uma constatação rápida. Se tomarmos
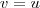
, então
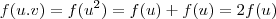
. Se tomarmos
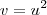
, então
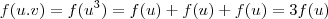
. Parece que, extrapolando essas operações,
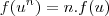
. Agora, a função que estamos manipulando está bem na cara! kk
Com isso podemos, num ato de, por hora, fé, extender a propriedade concebida para qualquer

inteiro de modo que
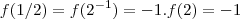
.
A última aplicação é trivial.
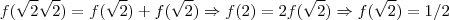
.
(:


 é a função calculada para o produto de
é a função calculada para o produto de  e
e  . Por exemplo, se
. Por exemplo, se 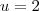 e
e 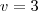 , então você calculará com esses valores
, então você calculará com esses valores 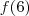 . Esta função possui uma propriedade interessante. Se você aplicar esta função em um produto a resposta(ou imagem) será a soma da aplicação dessa função em
. Esta função possui uma propriedade interessante. Se você aplicar esta função em um produto a resposta(ou imagem) será a soma da aplicação dessa função em 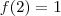 . Este é o ponto de partida. Para calcular as aplicações da função em outros números teremos de manipular este resultado.
. Este é o ponto de partida. Para calcular as aplicações da função em outros números teremos de manipular este resultado.  é, claramente, calculável. Note que, da propriedade,
é, claramente, calculável. Note que, da propriedade,  . Assim, rapidamente,
. Assim, rapidamente, 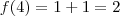 .
.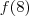 decorre, imediatamente, do resultado anterior. Podemos tomar
decorre, imediatamente, do resultado anterior. Podemos tomar 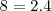 e teremos
e teremos 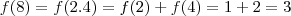 .
. não parece, a princípio, trivial. Mas, na realidade, é a mais trivial de todas. Note que
não parece, a princípio, trivial. Mas, na realidade, é a mais trivial de todas. Note que . Daí,
. Daí, 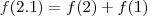 de onde
de onde . ( A essa altura já percebemos que as aplicações capturam numéros conhecido, não?)
. ( A essa altura já percebemos que as aplicações capturam numéros conhecido, não?)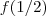 , que não aprece ser trivial. De fato, não é. Façamos uma constatação rápida. Se tomarmos
, que não aprece ser trivial. De fato, não é. Façamos uma constatação rápida. Se tomarmos 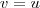 , então
, então 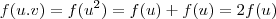 . Se tomarmos
. Se tomarmos 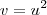 , então
, então 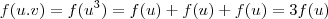 . Parece que, extrapolando essas operações,
. Parece que, extrapolando essas operações, 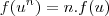 . Agora, a função que estamos manipulando está bem na cara! kk
. Agora, a função que estamos manipulando está bem na cara! kk inteiro de modo que
inteiro de modo que 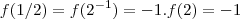 .
.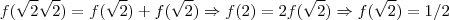 .
.
 , já q sempre
, já q sempre 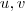 em
em 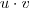 em
em  ,
, 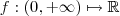 goza desta propriedade e
goza desta propriedade e  e
e  .
.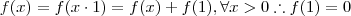 .
.
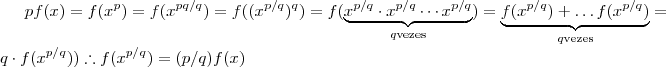
![0 = f(1) = f(x^{p/q-p/q}) = f(x^{p/q} \cdot x^{-p/q}) = f(x^{p/q}) + f(x^{-p/q}) = (p/q)f(x) + f(x^{-p/q}) \therefore [tex] f(x^{-p/q}) = (-p/q)x 0 = f(1) = f(x^{p/q-p/q}) = f(x^{p/q} \cdot x^{-p/q}) = f(x^{p/q}) + f(x^{-p/q}) = (p/q)f(x) + f(x^{-p/q}) \therefore [tex] f(x^{-p/q}) = (-p/q)x](/latexrender/pictures/61109b712b53bbab1f66336ad1a8f544.png)
 , teremos
, teremos 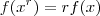 .
.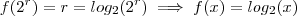
 é real, sendo
é real, sendo