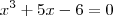por CJunior » Sex Fev 28, 2014 21:31
por CJunior » Sex Fev 28, 2014 21:31
( IME 1991) Mostre que
![\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} \sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/4621d3f2e07557a60e12af4abf134f60.png)
é um número racional.
-
CJunior
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Jan 26, 2014 13:18
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por young_jedi » Sáb Mar 01, 2014 13:40
por young_jedi » Sáb Mar 01, 2014 13:40
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Man Utd » Ter Mar 04, 2014 15:27
por Man Utd » Ter Mar 04, 2014 15:27
CJunior escreveu:( IME 1991) Mostre que
![\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} \sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/4621d3f2e07557a60e12af4abf134f60.png)
é um número racional.
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-\left(3-\sqrt[2]{9+\frac{125}{27}}\right)} x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-\left(3-\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/d09c32a8ff15ff88bcfa0477efae5cc1.png)
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}+\sqrt[3]{3-\sqrt[2]{9+\frac{125}{27}}} x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}+\sqrt[3]{3-\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/77177a6ce28bb1b576797645467a7e0d.png)
Perceba que agora está no "jeito" da
fórmula de cardano :
![x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}](/latexrender/pictures/e0348081b4cff83e57f4885ca16e4c4c.png)
que serve para resolver equações cúbicas reduzidas do tipo:

.Enfim comparando-a com a fórmula obtemos :
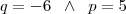
,segue que a equação é :
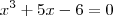
que já sabemos que a raiz real é

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por young_jedi » Ter Mar 04, 2014 22:01
por young_jedi » Ter Mar 04, 2014 22:01
fórmula de cardano,
muito bem observado Man Utd,
desse jeito fica mais simples valeu ai!!!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites com Raízes Cúbicas
por nathilopes » Qua Mar 05, 2014 02:23
- 2 Respostas
- 2907 Exibições
- Última mensagem por nathilopes

Qua Mar 05, 2014 16:09
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7443 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Como encontrar as raízes da Equação Cúbica
por DHST » Seg Nov 14, 2011 15:06
- 4 Respostas
- 2365 Exibições
- Última mensagem por DHST

Qua Nov 16, 2011 17:15
Sistemas de Equações
-
- log na base 1\5 de raiz cubica de 625 = 2x
por Nessa 2012 » Seg Nov 19, 2012 16:18
- 1 Respostas
- 3579 Exibições
- Última mensagem por Cleyson007

Seg Nov 19, 2012 16:31
Logaritmos
-
- Fatoração de raiz cúbica
por Paula Noia » Sáb Jun 15, 2013 21:22
- 2 Respostas
- 12285 Exibições
- Última mensagem por Paula Noia

Dom Jun 16, 2013 11:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} \sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/4621d3f2e07557a60e12af4abf134f60.png) é um número racional.
é um número racional.

![\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} \sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/4621d3f2e07557a60e12af4abf134f60.png) é um número racional.
é um número racional.
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/42e4a78c7c9a799820784f9158b35521.png)
![x^3=\left(\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}\right)^3 x^3=\left(\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}\right)^3](/latexrender/pictures/0cec8755c367c23ba189e46b4d76ef7b.png)
![x^3=3+\sqrt[2]{9+\frac{125}{27}}-3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}^2.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}+ x^3=3+\sqrt[2]{9+\frac{125}{27}}-3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}^2.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}+](/latexrender/pictures/f8be320e1d1c428ca694d2198f8ed70d.png)
![3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}^2+3-\sqrt[2]{9+\frac{125}{27}} 3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}^2+3-\sqrt[2]{9+\frac{125}{27}}](/latexrender/pictures/2018e273a87e55eabe40a2bb642bfdf1.png)
![x^3=6-3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}^2.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}+
3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}^2 x^3=6-3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}^2.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}+
3\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}.\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}^2](/latexrender/pictures/de6cab8bf20ef80c05601cc6da69f6a1.png)
![x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right)^2.\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}+ x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right)^2.\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}+](/latexrender/pictures/67c3956daadecc80ab808bc9705b0110.png)
![3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)^2} 3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)^2}](/latexrender/pictures/47d48d321d41bd2528ff1ca0ebede3ec.png)
![x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-3^2+\sqrt[2]{9+\frac{125}{27}}^2\right)} x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-3^2+\sqrt[2]{9+\frac{125}{27}}^2\right)}](/latexrender/pictures/9c3f7e9c135ae9f33d6327e47af24089.png)
![+3\sqrt[3]{\left(-3^2+\sqrt[2]{9+\frac{125}{27}}^2\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)} +3\sqrt[3]{\left(-3^2+\sqrt[2]{9+\frac{125}{27}}^2\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/1c70b5c34d72ba19cb91304c8f0aee48.png)
![x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-9+9+\frac{125}{27}\right)} x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\left(-9+9+\frac{125}{27}\right)}](/latexrender/pictures/d4679408c6ee6aec8e3be23408c890f6.png)
![+3\sqrt[3]{\left(-9+9+\frac{125}{27}\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)} +3\sqrt[3]{\left(-9+9+\frac{125}{27}\right).\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/65a6e634acbadb9e1f7ec746f42606b3.png)
![x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\frac{125}{27}} x^3=6-3\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right).\frac{125}{27}}](/latexrender/pictures/6f5a7686478aad5e6b4b2f154d4ea5c0.png)
![+3\sqrt[3]{\frac{125}{27}.\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)} +3\sqrt[3]{\frac{125}{27}.\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/2c0db777e137573bf1c66b63cda1c75c.png)
![x^3=6-3.\frac{5}{3}\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right)} x^3=6-3.\frac{5}{3}\sqrt[3]{\left(3+\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/61ab9e846a4a4cb2da6f25db49f18e57.png)
![+3.\frac{5}{3}\sqrt[3]{\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)} +3.\frac{5}{3}\sqrt[3]{\left(-3+\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/c1fb83baa7ce52866599158254cb0390.png)
![x^3=6-5\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}} x^3=6-5\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/83001e73f934d1ba9277db5cc317c668.png)
![+5\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}} +5\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/51c0051365f49ba476fea19d526992d4.png)
![x^3=6-5\left(\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}\right) x^3=6-5\left(\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}\right)](/latexrender/pictures/b6f3c439735d851f90fce3c65e8dcbe0.png)

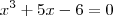
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}=1 x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-3+\sqrt[2]{9+\frac{125}{27}}}=1](/latexrender/pictures/83b7c07413c8b362c4adbf686417e54e.png)

é um número racional.
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-\left(3-\sqrt[2]{9+\frac{125}{27}}\right)} x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}-\sqrt[3]{-\left(3-\sqrt[2]{9+\frac{125}{27}}\right)}](/latexrender/pictures/d09c32a8ff15ff88bcfa0477efae5cc1.png)
![x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}+\sqrt[3]{3-\sqrt[2]{9+\frac{125}{27}}} x=\sqrt[3]{3+\sqrt[2]{9+\frac{125}{27}}}+\sqrt[3]{3-\sqrt[2]{9+\frac{125}{27}}}](/latexrender/pictures/77177a6ce28bb1b576797645467a7e0d.png)
![x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}](/latexrender/pictures/e0348081b4cff83e57f4885ca16e4c4c.png)
 .Enfim comparando-a com a fórmula obtemos :
.Enfim comparando-a com a fórmula obtemos : 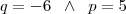 ,segue que a equação é :
,segue que a equação é :