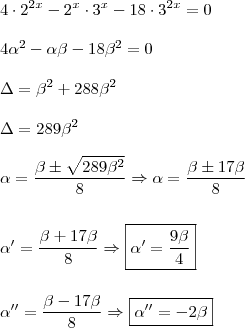por BrunoLima » Dom Nov 24, 2013 21:31
por BrunoLima » Dom Nov 24, 2013 21:31
Alguém pode dar uma sugestão? eu sei que tenho que dividir a equação, e depois fazer uma substituição.. bem foi o que o autor fez.. mas não estou conseguindo aplicar o conceito..
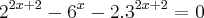
Então galera editando aqui.. eu dividi tudo por 6^x aí ficou
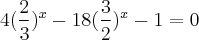
fazendo (2/3)^x = y eu econtrei a seguinte equação do segundo grau
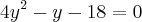
Ráizes= 9/4 e -2
-2 >> não convém 9/4 = (2/3)^x x=-2
Então galera eu consegui chegar a resposta do gabarito pois vi uma resolução parecida em um fórum e decidi tentar, como eu sou novo no fórum não sei muito bem o que fazer... se algum moderador quiser excluir tudo bem, se não, a questão está aí para quem estiver procurando, ou para alguém opinar uma resolução diferente..
-
BrunoLima
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Nov 22, 2013 23:52
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando militar
- Andamento: cursando
 por DanielFerreira » Seg Nov 25, 2013 00:00
por DanielFerreira » Seg Nov 25, 2013 00:00
Boa noite!
Inicialmente, devemos desenvolver a equação:
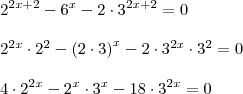
A fim de facilitar a visualização da equação, substituí
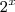
e

respectivamente por

e

, onde

é a variável e

uma constante qualquer, daí, resta-nos resolver a equação de grau 2.
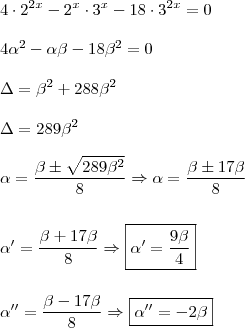
Já que concluiu/resolveu, não vejo por que terminar!
Até.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por BrunoLima » Seg Nov 25, 2013 00:09
por BrunoLima » Seg Nov 25, 2013 00:09
olá danrj, achei interessante sua resolução, Obrigado por ajudar ^^
-
BrunoLima
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Nov 22, 2013 23:52
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando militar
- Andamento: cursando
 por DanielFerreira » Sex Nov 29, 2013 00:13
por DanielFerreira » Sex Nov 29, 2013 00:13
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial Iezzi B.69
por BrunoLima » Sáb Nov 23, 2013 00:06
- 9 Respostas
- 5751 Exibições
- Última mensagem por Addlink1114

Ter Ago 18, 2015 04:56
Equações
-
- Equação exponencial iezzi 71
por BrunoLima » Sáb Nov 23, 2013 21:38
- 5 Respostas
- 2316 Exibições
- Última mensagem por BrunoLima

Dom Nov 24, 2013 00:00
Equações
-
- [Radiciação] livro 2 do Iezzi- exercicio
por edilviana » Qui Fev 16, 2012 11:39
- 1 Respostas
- 1771 Exibições
- Última mensagem por edilviana

Qui Fev 16, 2012 12:35
Álgebra Elementar
-
- Sistema de Equações exponenciais (iezzi)
por BrunoLima » Ter Nov 26, 2013 16:05
- 6 Respostas
- 3803 Exibições
- Última mensagem por e8group

Qua Nov 27, 2013 13:56
Equações
-
- Sistema de Equações exponenciais. iezzi
por BrunoLima » Ter Dez 03, 2013 16:12
- 3 Respostas
- 2191 Exibições
- Última mensagem por e8group

Qua Dez 04, 2013 14:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
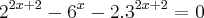
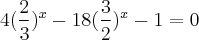
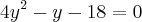


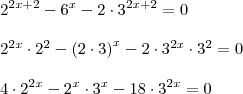
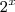 e
e  respectivamente por
respectivamente por  e
e  , onde
, onde