Segue a equação-exemplo:
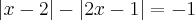

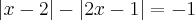

 nos quais ocorre a intersecção dos gráficos, mas pela definição também sai, tem que sair, só que deve-se aplicá-la duas vezes, uma para cada equação modular, vamos obter assim 4 equações, depois de resolvê-las validamos as respostas eliminando, eventualmente, as que não satisfazem a equação original.
nos quais ocorre a intersecção dos gráficos, mas pela definição também sai, tem que sair, só que deve-se aplicá-la duas vezes, uma para cada equação modular, vamos obter assim 4 equações, depois de resolvê-las validamos as respostas eliminando, eventualmente, as que não satisfazem a equação original.


 ) serve como solução, contrariando, assim, o gabarito oficial, que coloca na resposta a existência de dois elementos como solução, com
) serve como solução, contrariando, assim, o gabarito oficial, que coloca na resposta a existência de dois elementos como solução, com  . Há algum erro no procedimento?
. Há algum erro no procedimento?
 da seguinte forma:
da seguinte forma:


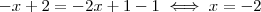
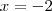 ou
ou 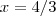

 . O problema é que se houvesse três ou mais "parcelas", tornaria o processo bastante trabalhoso.
. O problema é que se houvesse três ou mais "parcelas", tornaria o processo bastante trabalhoso.
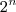 equações, sendo
equações, sendo  o número de módulos na expressão original.
o número de módulos na expressão original.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante