Seguinte, estou com um problema com uma demonstração, comecei mas fiquei "preso" em um ponto e aí vem a dúvida, estaria certo o que eu escrevi ?? Ou abordei de maneira errada o problema e por isso parei no ponto em questão ??? Segue o problema e a demonstração, ficarei imensamente grato se alguém verificasse para mim.
Problema:
Sejam A e B operadores auto-adjuntos tais que AB = BA. Mostre que existe uma única base ortonormal que diagonaliza simultaneamente A e B.
Demonstração que escrevi e parei:
Como AB = BA então A e B são operadores comutativos. Tenhamos
 um autovalor de A e
um autovalor de A e  o auto-espaço associado. Seja
o auto-espaço associado. Seja  tal que:
tal que: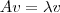
Então
 é invariante por B. Daí concluímos que v é um autovetor comum a A e a B, então:
é invariante por B. Daí concluímos que v é um autovetor comum a A e a B, então: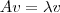

-----------------------------------------------
Eu acho que estou errando aqui, pois eu resolvi assumir um vetor
 tal que
tal que 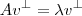
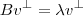
Daí eu concluo que
 pertence a uma base ortonormal... Parece que estou "forçando a barra" e por isso me soa como errado...
pertence a uma base ortonormal... Parece que estou "forçando a barra" e por isso me soa como errado...Alguém poderia me ajudar com essa demonstração ??
Desde já grato...
Renato.


 dois operadores auto-adjuntos tais que AB = BA, tenhamos
dois operadores auto-adjuntos tais que AB = BA, tenhamos 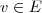 vetor não nulo tal que:
vetor não nulo tal que:
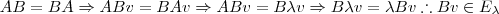
 tal que:
tal que: e
e  são ambos não invertíveis e como:
são ambos não invertíveis e como:
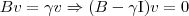
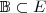 ortonormal de autovetores de A e B, logo a base
ortonormal de autovetores de A e B, logo a base 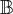 diagonaliza A e B simultaneamente.
diagonaliza A e B simultaneamente.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.