 por rhodry » Qui Nov 17, 2011 17:17
por rhodry » Qui Nov 17, 2011 17:17
Estou tendo dificuldades de resolver está inequação, se tiver alguém que puder me ajudar, agradeço....
2. Representemos por max(a, b) o maior dos números a e b. Resolva as inequações para
(3x^2+10x+8)/(x+2) < 2x +5
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 17:59
por MarceloFantini » Qui Nov 17, 2011 17:59
Quais foram suas tentativas?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhodry » Qui Nov 17, 2011 19:15
por rhodry » Qui Nov 17, 2011 19:15
Olá Marcelo, tentei determinar aplicando a regra de inequações do segundo, mas acabo me perdendo.....
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 19:47
por MarceloFantini » Qui Nov 17, 2011 19:47
Regra de inequações do segundo? Por favor, mostre seu desenvolvimento.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por TheoFerraz » Qui Nov 17, 2011 19:48
por TheoFerraz » Qui Nov 17, 2011 19:48
é o seguinte... temos :
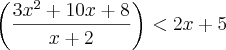
eis o seguinte fato indiscutível :
Seja P(x) um polinômio de grau n com pelomenos uma raiz real  . Entao o polinômio é divisível por
. Entao o polinômio é divisível por  , em outras palavras, o quociente
, em outras palavras, o quociente 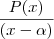 é inteiro (não tem resto)
é inteiro (não tem resto) verifique que no seu caso voce tem uma divisão desse tipo!!!
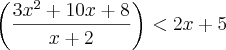
o polinomio
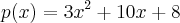
tem como uma de suas raizes o -2!!
entao voce pode dividir sem medo o lado esquerdo da equação. (lembrando sempre da condição que x tem que ser diferente de -2 na sua equação, senão estariamos dividindo por zero)
por fim obtemos:
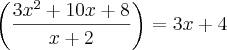
se eu nao tiver cometido nenhum erro na divisão.
Agora, o que nos resta é:
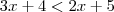
que vira

perceba que nessa solução o valor x = -2 é valido!
mas como nós efetuamos uma divisão lá em cima, se não me engano é preciso tirar esse -2 da solução, nos deixando com:

.
Editado pela última vez por
TheoFerraz em Qui Nov 17, 2011 19:55, em um total de 1 vez.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Qui Nov 17, 2011 19:49
por TheoFerraz » Qui Nov 17, 2011 19:49
OBS:desculpa, entrei no meio da conversa de vocês... De fato, mostrar o seu desenvolvimento seria legal, também por que eu também não compreendi "regras de inequação de segundo"
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por rhodry » Qui Nov 17, 2011 20:30
por rhodry » Qui Nov 17, 2011 20:30
sim Theo, está era a minha dúvida, devido o valor negativo, pelo que tenho pesquisado era citado a questão da inequação modular, então não sabia como determinar, vendo que vc cita a questão x pertencendo aos reais, com x diferente de -2, estava tentando demonstrar com regras de sinais "varal" mas agora está claro.... desde já agradeço á todos,,,,,,
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequações
por Bruno 888 » Qua Set 24, 2008 20:36
- 1 Respostas
- 4203 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:09
Inequações
-
- Inequações
por Rose » Seg Nov 24, 2008 22:44
- 2 Respostas
- 3689 Exibições
- Última mensagem por Rose

Qua Nov 26, 2008 08:18
Inequações
-
- Inequações
 por cristina » Seg Set 07, 2009 01:46
por cristina » Seg Set 07, 2009 01:46
- 2 Respostas
- 2915 Exibições
- Última mensagem por cristina

Seg Set 07, 2009 20:55
Sistemas de Equações
-
- inequações
por jose henrique » Ter Out 26, 2010 23:56
- 10 Respostas
- 6806 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 10:31
Sistemas de Equações
-
- Inequações
por brijahh » Sáb Ago 06, 2011 10:38
- 1 Respostas
- 2198 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 06, 2011 17:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







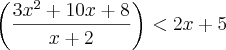
 . Entao o polinômio é divisível por
. Entao o polinômio é divisível por  , em outras palavras, o quociente
, em outras palavras, o quociente 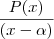 é inteiro (não tem resto)
é inteiro (não tem resto) 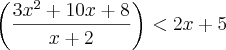
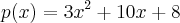
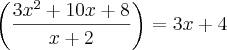
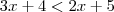







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.