 por victorleme » Ter Mai 03, 2011 11:20
por victorleme » Ter Mai 03, 2011 11:20
1- p e q são números inteiros,positivos e relativamente primos, , qual é o valor de p+q?
, qual é o valor de p+q?Minha primeira dúvida, o que ele quer dizer com números "relativamente primos", números próximos?
No gabarito ele fala que a resposta de p+q é igual a 19, mas se substituirmos não chegamos a esse valor.
2-) X=![\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} \sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}}](/latexrender/pictures/f0a7b26744dbb549ecbb6e04fc72fe80.png) , prove que x é um número real.
, prove que x é um número real.Esse realmente não sei por onde começar.
-
victorleme
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 23, 2011 19:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecatrônica
- Andamento: cursando
 por Abelardo » Ter Mai 03, 2011 15:56
por Abelardo » Ter Mai 03, 2011 15:56
No final eu disse ''provando'', é melhor entender que ''encontramos'' um valor real para x.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por victorleme » Ter Mai 03, 2011 19:06
por victorleme » Ter Mai 03, 2011 19:06
Abelardo escreveu:1) ''Relativamente primos'' quer dizer que são primos entre si, o único número inteiro e positivo que divide p e q é 1.
Não compreendi, quer dizer que o MDC deles seria 1?
O valor de p e q seria 12 e 7 respectivamente? Mas não seria somente o 7 primo?
Aqui, por que você multiplicou por 1?

-
victorleme
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 23, 2011 19:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecatrônica
- Andamento: cursando
 por Abelardo » Ter Mai 03, 2011 20:05
por Abelardo » Ter Mai 03, 2011 20:05
Não compreendi, quer dizer que o MDC deles seria 1? A resposta é sim. Há algum outro número inteiro e positivo que divide 12 e 7? Não, não há.
O valor de p e q seria 12 e 7 respectivamente? Sim. Mas para resolver a questão isso é um tanto relevante. Veja que ele quer saber o resultado de p + q; a ordem das parcelas não altera a soma. Tenha em mente que precisávamos encontrar uma fração irredutível e depois somar as suas partes.
Mas não seria somente o 7 primo? Não é bem isso. Você está confundindo número primo com primos relativos. Sete é sim um número primo e doze não, mas quando procuramos um número que divida doze e sete simultaneamente só encontramos 1 e nesses casos dizemos que doze e sete são primos entre si.
Aqui, por que você multiplicou por 1?

Quando temos uma fração dividindo outra o que devemos fazer? Multiplicar a primeira fração pelo inverso da segunda. Fiz isso nessa parte -->

. Depois apliquei a propriedade e ficou assim


-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por victorleme » Qua Mai 04, 2011 00:54
por victorleme » Qua Mai 04, 2011 00:54
Aopa!
Esclareceu tudo!
-
victorleme
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 23, 2011 19:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecatrônica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17178 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 4103 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
-
- Numeros Primos
por Neperiano » Sex Abr 24, 2009 20:15
- 6 Respostas
- 5718 Exibições
- Última mensagem por Neperiano

Sáb Abr 25, 2009 10:23
Problemas do Cotidiano
-
- Números Primos
por Abelardo » Qua Mar 09, 2011 21:38
- 1 Respostas
- 3056 Exibições
- Última mensagem por Abelardo

Qua Mar 09, 2011 21:41
Álgebra Elementar
-
- OBM - Números primos
por Abelardo » Sáb Mar 12, 2011 16:54
- 4 Respostas
- 4683 Exibições
- Última mensagem por Abelardo

Dom Mar 13, 2011 13:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , qual é o valor de p+q?
, qual é o valor de p+q?![\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} \sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}}](/latexrender/pictures/f0a7b26744dbb549ecbb6e04fc72fe80.png) , prove que x é um número real.
, prove que x é um número real.





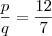 logo 12 + 7 = 19.
logo 12 + 7 = 19.![X=\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} X=\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}}](/latexrender/pictures/23c83ac60df05cc04ff49ff77eac1239.png) . Podemos elevar ambos os lado ao quadrado.
. Podemos elevar ambos os lado ao quadrado. ![X^2=\left(\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} \right)^2 X^2=\left(\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} \right)^2](/latexrender/pictures/44ca95b6a6378ed7132f2dc083f03f5c.png) --->
--->![X^2= 6 + \sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}} X^2= 6 + \sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+\sqrt[2]{6+....}}}}](/latexrender/pictures/18a76beaa8defcd7961adfe74224cc88.png) , agora perceba que no segundo membro da equação temos seis somado a '' X ''. Ficamos com
, agora perceba que no segundo membro da equação temos seis somado a '' X ''. Ficamos com 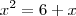 , ai é só passar o seis e o x para o primero membro e resolver a equação do segundo grau. Você encontrará duas raízes reais, uma negativa e outra positiva, mas lembrando que
, ai é só passar o seis e o x para o primero membro e resolver a equação do segundo grau. Você encontrará duas raízes reais, uma negativa e outra positiva, mas lembrando que ![\sqrt[2]{x^2}= \left|x \right| \sqrt[2]{x^2}= \left|x \right|](/latexrender/pictures/141bfaeb2e7f8d52454c40e90651a2fc.png) ... logo só sobrará a raiz positiva que é 3; provando assim que x é número real.
... logo só sobrará a raiz positiva que é 3; provando assim que x é número real.






