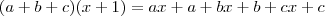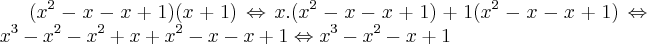por lucas7 » Seg Fev 21, 2011 21:37
por lucas7 » Seg Fev 21, 2011 21:37
Tenho mais uma pergunta:
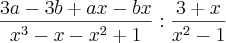
Fatorando cheguei até:
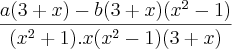
Até aí está certo? Como prossigo? O gabarito diz
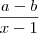
obrigado novamente
Editado pela última vez por
lucas7 em Seg Fev 21, 2011 23:08, em um total de 1 vez.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Seg Fev 21, 2011 23:08
por LuizAquino » Seg Fev 21, 2011 23:08
Veja se o tópico abaixo ajuda:
Dúvida na Fatoraçãoviewtopic.php?f=68&t=3842
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucas7 » Seg Fev 21, 2011 23:46
por lucas7 » Seg Fev 21, 2011 23:46
O denominador da questão então seria
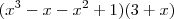
que equivale a
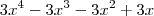
, para eu deduzir uma raiz eu faria
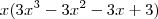
,
"Basta substituir x por (-3 no caso) nessa equação e você verá que ela é válida. " não caiu a ficha muito bem, mas fiz
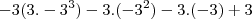
deu -42.
Como (-3) é uma raíz, você pode reduzir o grau desse polinômio para achar as outras duas raízes. Para isso, você pode dividir o polinômio por (x+3).
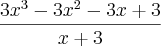
Mas acho que já me perdi completamente, tem como você explicar de uma maneira diferente, por favor? Obrigado
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 00:05
por LuizAquino » Ter Fev 22, 2011 00:05
Exercício: Fatore
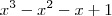
.
Para fatorar esse polinômio você precisa encontrar as raízes da equação:
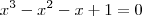
Note que 1 é raiz dessa equação, pois substituindo x por 1 nós teremos:
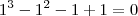
Para achar as outras raízes, podemos reduzir o grau do polinômio. Para isso, divida o polinômio por (x-1). Nesse caso, você vai obter
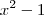
. Agora, obtendo as raízes de
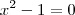
, nós teremos x'=1 e x''=-1.
Portanto, as raízes desse polinômio são x' = 1, x'' = 1, x'''= -1.
A forma fatorada do polinômio será:
![x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1) x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1)](/latexrender/pictures/c5784f486c1cf1f85e3c2f8a547bc0be.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucas7 » Ter Fev 22, 2011 16:28
por lucas7 » Ter Fev 22, 2011 16:28
Ok. Após horas queimando meus neurônios, consegui entender, parcialmente.
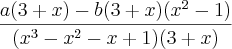
=
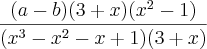
=
Fatorando
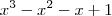
por (x-1) para reduzir o grau do polinômio
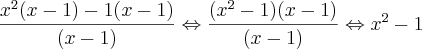
Bháskara de
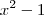
, achei as raízes 1 e -1, e já tenho a outra raíz 1 que usei para reduzir o grau do polinômio.

obs: teoricamente isso já seria suficiente para eu resolver a questão, pois

(resposta do gabarito)
Porém, eu fiz o teste e multipliquei

, para ver se seria igual a
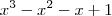
e não dá.
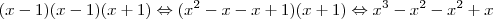
qual o meu erro? porque que essa multiplicação não está dando
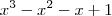
????
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 16:56
por LuizAquino » Ter Fev 22, 2011 16:56
lucas7 escreveu:Porém, eu fiz o teste e multipliquei (x-1)(x-1)(x+1), para ver se seria igual a
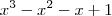
e não dá.
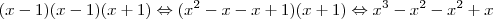
qual o meu erro? porque que essa multiplicação não está dando
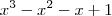
????
Você esqueceu de aplicar a distributiva multiplicando o 1 por cada termo do fator
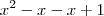
. Você apenas aplicou a distributiva multiplicando cada termo do fator
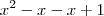
por x.
Editado pela última vez por
LuizAquino em Ter Fev 22, 2011 17:00, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucas7 » Ter Fev 22, 2011 17:00
por lucas7 » Ter Fev 22, 2011 17:00
Tem como você exemplificar fazendo

passo a passo? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
Editado pela última vez por
lucas7 em Ter Fev 22, 2011 17:08, em um total de 2 vezes.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 17:03
por LuizAquino » Ter Fev 22, 2011 17:03
lucas7 escreveu:Tem como você exemplificar? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
Qual é o resultado de aplicar a distributiva em
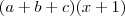
?
Fazendo a distributiva:
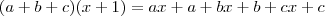
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucas7 » Ter Fev 22, 2011 17:08
por lucas7 » Ter Fev 22, 2011 17:08
Entendi:
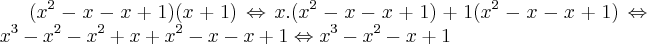
É isso professor?
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 17:17
por LuizAquino » Ter Fev 22, 2011 17:17
lucas7 escreveu:Entendi:
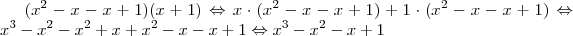
É isso professor?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucas7 » Ter Fev 22, 2011 17:26
por lucas7 » Ter Fev 22, 2011 17:26
Refiz a questão desde o início e consegui graças aos novos conhecimentos que obtive com sua ajuda, muito obrigado


O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de fração algébrica
por lucas7 » Seg Fev 21, 2011 18:09
- 3 Respostas
- 2410 Exibições
- Última mensagem por lucas7

Seg Fev 21, 2011 22:16
Álgebra Elementar
-
- Fração Algébrica
por Lucio » Qua Dez 21, 2011 07:48
- 3 Respostas
- 2172 Exibições
- Última mensagem por fraol

Qua Dez 21, 2011 22:31
Polinômios
-
- Fração algébrica
por LuizCarlos » Sex Abr 20, 2012 13:09
- 5 Respostas
- 2314 Exibições
- Última mensagem por Cleyson007

Sex Abr 20, 2012 17:44
Álgebra Elementar
-
- Re: Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 09:10
- 5 Respostas
- 2590 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 16:44
Álgebra Elementar
-
- Fração algébrica
por LuizCarlos » Sáb Abr 21, 2012 19:04
- 6 Respostas
- 2880 Exibições
- Última mensagem por Russman

Sáb Abr 21, 2012 20:40
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
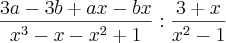
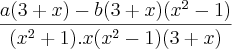
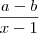

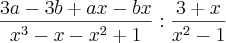
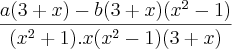
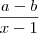


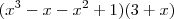 que equivale a
que equivale a 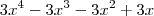 , para eu deduzir uma raiz eu faria
, para eu deduzir uma raiz eu faria 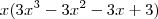 ,
,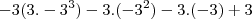 deu -42.
deu -42.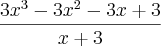

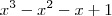 .
.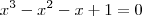
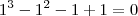
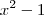 . Agora, obtendo as raízes de
. Agora, obtendo as raízes de 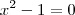 , nós teremos x'=1 e x''=-1.
, nós teremos x'=1 e x''=-1.![x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1) x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1)](/latexrender/pictures/c5784f486c1cf1f85e3c2f8a547bc0be.png)

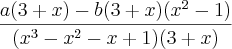 =
= =
=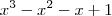 por (x-1) para reduzir o grau do polinômio
por (x-1) para reduzir o grau do polinômio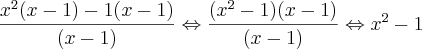
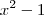 , achei as raízes 1 e -1, e já tenho a outra raíz 1 que usei para reduzir o grau do polinômio.
, achei as raízes 1 e -1, e já tenho a outra raíz 1 que usei para reduzir o grau do polinômio.
 (resposta do gabarito)
(resposta do gabarito) , para ver se seria igual a
, para ver se seria igual a 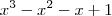 e não dá.
e não dá.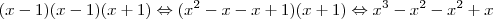 qual o meu erro? porque que essa multiplicação não está dando
qual o meu erro? porque que essa multiplicação não está dando 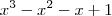 ????
????
e não dá.
qual o meu erro? porque que essa multiplicação não está dando
????
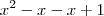 . Você apenas aplicou a distributiva multiplicando cada termo do fator
. Você apenas aplicou a distributiva multiplicando cada termo do fator 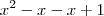 por x.
por x.
 passo a passo? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
passo a passo? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
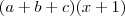 ?
?