se n é o número real
 , responda, justificando, qual das expressões a seguir representa o maior número.
, responda, justificando, qual das expressões a seguir representa o maior número.a) 5+n
b) 5-n
c)5.n
d)5/n
e)n/5
meu raciocínio foi que se n=1
5+1=6
5-1=4
5.1=5
5/1=5
1/5=1/5
neste caso seria a alternativa a, porém se mudarmos o valor de n para 2 a alternativa correta seria c.
alguém pode me ajudar pois eu não sei se o meu entendimento está correto
desde agradeço



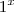 é
é  para qualquer x.
para qualquer x.
 .
.
 :
: