 por anneliesero » Ter Set 25, 2012 21:49
por anneliesero » Ter Set 25, 2012 21:49
Pessoal, nessa questão qual foi o meu erro?
(UFBA) A matriz 2X3, com
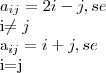
é:
a)
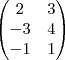
b)
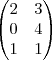
c)
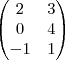
d)
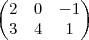
e)
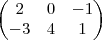
A alternativa certa é a D.
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Set 25, 2012 22:11
por MarceloFantini » Ter Set 25, 2012 22:11
Onde está o que você fez, para que possamos identificar o erro?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anneliesero » Qua Set 26, 2012 14:20
por anneliesero » Qua Set 26, 2012 14:20
O meu cálculo é o seguinte:
2 linhas e 3 colunas
Então a fórmula usada será

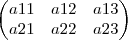
a11=2.1-1=1
a12=2.1-2=2-2=0
a13=2.1-3=2-3=-1
a21=2.2-1=4-1=3
a22= 2.2-2=4-2=2
a23=2.2-3=4-3=1
Com isso a matriz ficará assim:
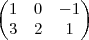
Mas, a minha resposta não tem alternativa.

''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qua Set 26, 2012 15:15
por young_jedi » Qua Set 26, 2012 15:15
essa equação que voce utilizou

só vale para os elemntos em que i é diferente de j
para os elementos que em que i é igual a j a equação é

então

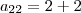
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por anneliesero » Qui Set 27, 2012 18:14
por anneliesero » Qui Set 27, 2012 18:14
Sim, foi essa a equação
2i-j
Mas i não é o nº de linhas? E j o nº de colunas?
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Set 27, 2012 18:21
por young_jedi » Qui Set 27, 2012 18:21
Sim é i o numero da linha e j o de coluna
mais repare no enunciado que voce tem duas equações diferentes,uma para quando i é diferente de j
e uma para quando i é igual a j.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por anneliesero » Qui Set 27, 2012 20:35
por anneliesero » Qui Set 27, 2012 20:35
Mas no enunciado não fala que a matriz 2x3. Com isso 2 é o nº de linhas e 3 nº de colunas. Certo?
Consequentemente eliminados as outras alternativas que não atendam a matriz de 2 linhas e 3 colunas. E usamos a fórmula do diferente. Não é?
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Set 27, 2012 20:42
por young_jedi » Qui Set 27, 2012 20:42
para cada elemento da matriz que voce vai calcular voce tem que analisar o i e o j.
para o elemento

temos que i=1 e j=1 portanto i=j então voce utiliza a equação
i+j, já para o elemento
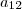
temos que i=1 e j=2 então
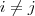
então voce utiliza a equação
2i-j.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por anneliesero » Qui Set 27, 2012 20:57
por anneliesero » Qui Set 27, 2012 20:57
ahh agora entendi valeu muito obrigada

''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5153 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3595 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 5997 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9687 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12793 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
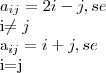
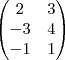
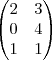
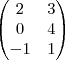
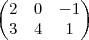
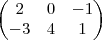

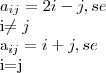
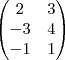
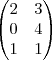
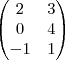
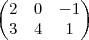
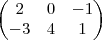



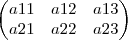
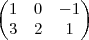





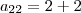




 temos que i=1 e j=1 portanto i=j então voce utiliza a equação
temos que i=1 e j=1 portanto i=j então voce utiliza a equação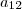 temos que i=1 e j=2 então
temos que i=1 e j=2 então 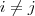 então voce utiliza a equação
então voce utiliza a equação


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)