 por Mic_17 » Qua Ago 22, 2012 17:03
por Mic_17 » Qua Ago 22, 2012 17:03
Por favor, preciso de ajuda com essa questão!!!
(Unifal-MG) Seja a circunferencia C de equação x^2+y^2+6raiz(3)x-6y+27=0. Determine a abscissa e a ordenada do ponto P de C que esteja o mais próximo possível da origem do sistema de coordenadas cartesianas.
Minha resolução:
* d(CO)=raiz((-3raiz(3))^2 + (3)^2 = raiz(9.3+9) = raiz(36) = d(CO)= 6 (distancia do centro C a origem O é 6.)
* Descobrir coeficiente angular da reta CO: m=y-yi/x-xi = 3-0/-3raiz(3)-0 = 3/-3raiz(3) = -raiz(3)
* equação reduzida da reta: y = mx -> y = -raiz(3)x
Daí eu tento substituir na equação da circunferencia mas o resultado não dá certo!!
A resposta é: xp=-3raiz(3)/2 e yp=3/2
-
Mic_17
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Ago 22, 2012 16:52
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3ano
- Andamento: cursando
 por Russman » Qua Ago 22, 2012 23:42
por Russman » Qua Ago 22, 2012 23:42
Suponhamos que o ponto

seja
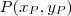
. Assim, a distância desse ponto até o Origem é
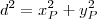
.
Ainda, sabemos que esse ponto deve satisfazer a equação da circunferência
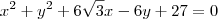
.
Assim, temos de solucionar o sistema
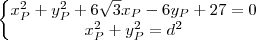
que é, na verdade, a busca do ponto de intersecção entre duas circunferências! Combinando as equações e tentando expressar uma equação em

na presença de

, temos, substituindo

na primeira( a apartir de agora simplificarei a notação para
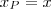
e
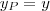
.)
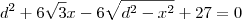
de onde chegamos em
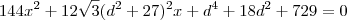
.
Lembre-se que qeremos que esta equação tenha apenas 1 solução. Logo, o discriminante da mesma, o Delta, deve ser nulo. Fazendo isso, chega-se a equação em

.
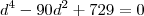
a qual apresenta duas soluções possíveis:

ou

. Como qeremos a menor, tomamos

.
Se

a equação
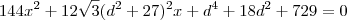
se transforma em
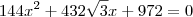
a qual tem duas soluções iguais
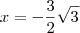
.
Agora basta calcular

. De
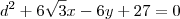
temos
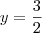
como resposta.
Logo o ponto é
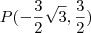
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1884 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Circunferência
por ilovemat » Sex Abr 03, 2009 19:12
- 5 Respostas
- 9515 Exibições
- Última mensagem por Marcampucio

Seg Abr 06, 2009 20:11
Trigonometria
-
- circunferência
por jeffersonricardo » Seg Set 06, 2010 15:20
- 7 Respostas
- 4362 Exibições
- Última mensagem por MarceloFantini

Seg Set 06, 2010 17:14
Geometria Analítica
-
- circunferencia
 por cosme » Qua Nov 17, 2010 09:29
por cosme » Qua Nov 17, 2010 09:29
- 2 Respostas
- 1833 Exibições
- Última mensagem por MarceloFantini

Qua Nov 17, 2010 15:11
Trigonometria
-
- Circunferência
por Pri Ferreira » Qua Nov 09, 2011 21:02
- 1 Respostas
- 1310 Exibições
- Última mensagem por LuizAquino

Qui Nov 10, 2011 20:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 seja
seja 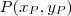 . Assim, a distância desse ponto até o Origem é
. Assim, a distância desse ponto até o Origem é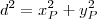 .
.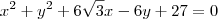 .
.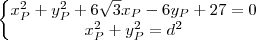
 na presença de
na presença de  , temos, substituindo
, temos, substituindo  na primeira( a apartir de agora simplificarei a notação para
na primeira( a apartir de agora simplificarei a notação para 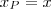 e
e 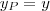 .)
.)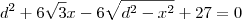
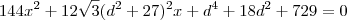 .
.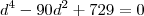
 ou
ou  . Como qeremos a menor, tomamos
. Como qeremos a menor, tomamos 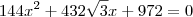 a qual tem duas soluções iguais
a qual tem duas soluções iguais 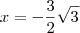 .
.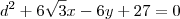 temos
temos 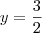 como resposta.
como resposta.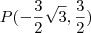 .
.