Por favor, preciso de ajuda com essa questão!!!
(Unifal-MG) Seja a circunferencia C de equação x^2+y^2+6raiz(3)x-6y+27=0. Determine a abscissa e a ordenada do ponto P de C que esteja o mais próximo possível da origem do sistema de coordenadas cartesianas.
Minha resolução:
* d(CO)=raiz((-3raiz(3))^2 + (3)^2 = raiz(9.3+9) = raiz(36) = d(CO)= 6 (distancia do centro C a origem O é 6.)
* Descobrir coeficiente angular da reta CO: m=y-yi/x-xi = 3-0/-3raiz(3)-0 = 3/-3raiz(3) = -raiz(3)
* equação reduzida da reta: y = mx -> y = -raiz(3)x
Daí eu tento substituir na equação da circunferencia mas o resultado não dá certo!!
A resposta é: xp=-3raiz(3)/2 e yp=3/2


 seja
seja 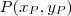 . Assim, a distância desse ponto até o Origem é
. Assim, a distância desse ponto até o Origem é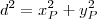 .
.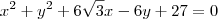 .
.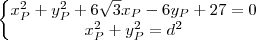
 na presença de
na presença de  , temos, substituindo
, temos, substituindo  na primeira( a apartir de agora simplificarei a notação para
na primeira( a apartir de agora simplificarei a notação para 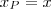 e
e 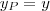 .)
.)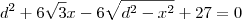
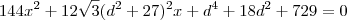 .
.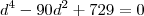
 ou
ou  . Como qeremos a menor, tomamos
. Como qeremos a menor, tomamos 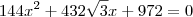 a qual tem duas soluções iguais
a qual tem duas soluções iguais 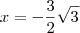 .
.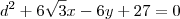 temos
temos 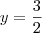 como resposta.
como resposta.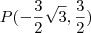 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.