Boa noite... Gostaria de uma dica, ajuda com a seguinte questão:
Encontrar os vetores unitários paralelos ao plano yOz e que são ortogonais ao vetor v = (4, 1, -2).
Minha dúvida é em relação a informação ''... unitários paralelos ao plano yOz''



felipe10 escreveu:Minha dúvida é em relação a informação ''... unitários paralelos ao plano yOz''
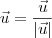
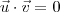 . Há infinitas soluções . Tente concluir .
. Há infinitas soluções . Tente concluir .

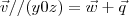 ,
, são dos seguintes formatos ,
são dos seguintes formatos , (Variação apenas para "y") e
(Variação apenas para "y") e  (Variação apenas para "z") donde ,
(Variação apenas para "z") donde ,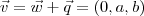

 tem por equação
tem por equação  . Veja, que o vetor normal esse plano é o vetor
. Veja, que o vetor normal esse plano é o vetor  , isto é, o proóprio vetor
, isto é, o proóprio vetor 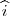 .
.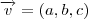 deve ser paralelo ao plano
deve ser paralelo ao plano  então este deve ser perpendicular ao vetor normal desse plano. Em outras palavras, é necessário que o produto interno de
então este deve ser perpendicular ao vetor normal desse plano. Em outras palavras, é necessário que o produto interno de 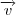 e
e 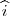 seja nulo!
seja nulo!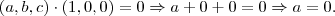
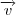 para ser paralelo ao plano
para ser paralelo ao plano  deve ter a primeira componente nula!
deve ter a primeira componente nula! .
.
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.