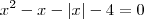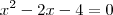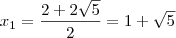Eis que não aprendi muito sobre módulos, e me deparo com o seguinte exercício da PUC-MG:
A soma das raízes da equação: x² - x - |x| - 4 = 0
A resposta é:
![\sqrt[2]{5} - 1 \sqrt[2]{5} - 1](/latexrender/pictures/34a78f4899ffca6ff4ec34d80bf5e040.png)
Ao realizar meus cálculos levei em consideração a propriedade modular que diz que: |x|² = |x²| = x²
então mudei a equação principal para |x|² - x - |x| - 4 = 0
A partir daí não sei se posso colocar o outro x em módulo... Mesmo assim tentei, então ficou:
|x|² - |x| - |x| - 4 = 0 , Substitui |x| por y , e fiz a resolução normalmente:
y² - 2y - 4 = 0 , Raízes: y' =
![\frac{2 + 2\sqrt[2]{5}}{2} \frac{2 + 2\sqrt[2]{5}}{2}](/latexrender/pictures/5bf0273de34b495af83e156340ad1bf6.png) e y" =
e y" = ![\frac{2 - 2\sqrt[2]{5}}{2} \frac{2 - 2\sqrt[2]{5}}{2}](/latexrender/pictures/5a53b43643f284f65388221ff0704033.png)
Agora não sei como continuar... poderiam me ajudar?