 por karinak » Sáb Jun 16, 2012 02:08
por karinak » Sáb Jun 16, 2012 02:08
Sou iniciante em calculo e me deparei com a seguinte questão (cos x.senx )/(tg x), não sei como aplicar as duas fórmulas ao mesmo tempo.
Obrigada pela atenção!
-
karinak
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 15, 2012 23:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Jhonata » Sáb Jun 16, 2012 10:58
por Jhonata » Sáb Jun 16, 2012 10:58
karinak escreveu:Sou iniciante em calculo e me deparei com a seguinte questão (cos x.senx )/(tg x), não sei como aplicar as duas fórmulas ao mesmo tempo.
Obrigada pela atenção!
Bom dia!
Nessa situação você terá que aplicar a regra da Cadeia.
Reconheça a identidade

e a reescreva como:
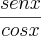
.
Assim, vamos obter:

. Podemos fazer um cancelamento e ficaremos apenas com
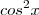
.
Tente derivar agora.
OBS: Eu acho que em questões que envolvem expressões trigonométricas, dificilmente será pedido pra usar os dois ao mesmo tempo, até porque é um pouco complicado. De qualquer forma, se você quiser aplicar essas regras, você poderia desmembrar o integrando, mas daria muito trabalho.
Por exemplo:
Reescreveria a expressão assim:
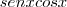
*

e aplicar a regra do produto fazendo f(x)=senxcosx e g(x)=1/tgx, mas nessa aplicação você aplicaria várias vezes a regra dentro de regra, o que seria muito trabalhoso.
Abraços.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por karinak » Sáb Jun 16, 2012 12:43
por karinak » Sáb Jun 16, 2012 12:43
Obrigada pela ajuda, deu para esclarecer bastante as minhas dúvidas.Essa questão foi de uma prova do semestre passado, estou refazendo caso a proff as repita.
-
karinak
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 15, 2012 23:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Funciona para produto mas não para quociente?
por Matheus Lacombe O » Ter Dez 11, 2012 23:46
- 1 Respostas
- 2189 Exibições
- Última mensagem por Russman

Qua Dez 12, 2012 01:39
Cálculo: Limites, Derivadas e Integrais
-
- inequação produto/quociente
por vhcs29 » Qui Abr 01, 2010 12:32
- 2 Respostas
- 5299 Exibições
- Última mensagem por vhcs29

Sex Abr 02, 2010 12:59
Álgebra Elementar
-
- Produtos Notáveis - como aplicar nesta equação
por fcomex » Ter Mai 20, 2014 00:15
- 1 Respostas
- 1304 Exibições
- Última mensagem por fcomex

Ter Mai 20, 2014 01:13
Álgebra Elementar
-
- Como aplicar o metodo de Gauss Jordan nesse sistema.
por 380625 » Sáb Ago 20, 2011 16:19
- 3 Respostas
- 6088 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 22:26
Sistemas de Equações
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12550 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e a reescreva como:
e a reescreva como: 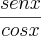 .
. . Podemos fazer um cancelamento e ficaremos apenas com
. Podemos fazer um cancelamento e ficaremos apenas com 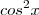 .
.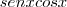 *
*  e aplicar a regra do produto fazendo f(x)=senxcosx e g(x)=1/tgx, mas nessa aplicação você aplicaria várias vezes a regra dentro de regra, o que seria muito trabalhoso.
e aplicar a regra do produto fazendo f(x)=senxcosx e g(x)=1/tgx, mas nessa aplicação você aplicaria várias vezes a regra dentro de regra, o que seria muito trabalhoso.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.