Bom o meu problema esta relacionado principalmente ao cálculo do intervalo de confiança, ou como
calcular o z, t ou que valores preciso utilizar das tabelas de gauss e student. Um exemplo:
Uma fábrica de lajotas de cerâmica introduz um novo material em sua fabricação e acredita que
aumentará a resistência média, que é de 206kg. A resistência das lajotas tem distribuição normal
com desvio padrão de 12kg. Retira-se uma amostra de 30 lajotas, obtendo média amostral igual a
210kg. Ao nível de 10%, pode o fabricante aceitar que a resistência média de suas lajotas tenha
aumentado?
Eu sei que:
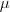= 206 Kg
=12 Kgn = 30 lajotas
x= 210 Kg
=10%E que resolvendo ficaria assim:
![z = \frac{x - 206}{\frac{12}{\sqrt[]{30}}}](/latexrender/pictures/0eef4296d87fd7e867f0c871e869e8ec.png "z = \frac{x - 206}{\frac{12}{\sqrt[]{30}}}")
Mas e o valor de z ??
Meu professor resolveu com z=1,282 mas de onde ele tirou esse valor? Que cálculo fazer? Como achar o intervalo de segurança?
Muitíssimo obrigada a quem puder me ajudar.
Um bom feriado!
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.