 por Magda » Sex Jun 19, 2009 18:37
por Magda » Sex Jun 19, 2009 18:37
Como resolvo este sistema?
2. (x+y) = x + 3
y+3 = 3. (x-y)
já tentei resolver de algumas formas, mas não consegui. Tentei pela regua de Cramer e depois tentei isolar uma das incógnitas. Ao final tem que se descobrir o valor de (x+y)ao quadrado. O resultado dá 5 19/25. O meu resultado de 81!!
-
Magda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 19, 2009 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
 por Marcampucio » Sex Jun 19, 2009 19:14
por Marcampucio » Sex Jun 19, 2009 19:14
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Magda » Sex Jun 19, 2009 19:36
por Magda » Sex Jun 19, 2009 19:36
Grata pela resposta!!
-
Magda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 19, 2009 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
 por Magda » Qui Ago 06, 2009 18:32
por Magda » Qui Ago 06, 2009 18:32
No dia 19 de Junho, recebi a reslução do sistema 2(x+y)= x+3
y+3= 3(x-Y)
quanto a resolução da primeira sentença, não houve dúvidas, já quanto a resolução da segunda, não entendi as alterações de sinais:
y+3 = 3(x-y)
y+3 = 3x - 3y (até aqui ok)
3x - 4y - 3 = 0
(se o y está de um lado e o -3y do outro, como podemos somá-los resultando em -4y? Da mesma forma, porque o 3 fica negativo, se é positivo e se foi passado para o lado contrário, porque o 3x não mudou de sinal? Ou não necessário alterar o sinal quando passamos para o outro lado? Ficaria: y +3 -3x + 3y = 0
-3x +4y +3 = 0
e daí, não chego mais ao resultado esperado que é (x+y)² = 5 19/5
Gostaria de mais uma explicação, pois preciso ensinar para minha filha que está na oitava série.
Grata,
Magda
-
Magda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 19, 2009 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
 por Marcampucio » Qui Ago 06, 2009 20:53
por Marcampucio » Qui Ago 06, 2009 20:53
Cara Magda,
note que uma igualdade não se altera se efetuarmos em ambos os membros a mesma operação:

1- adição

o valor em cada lado muda, mas a
igualdade se mantém.
2- subtração

3- multiplicação

4- divisão

é isso que foi feito na passagem em que você teve dúvidas:

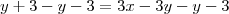
em cada lado foram subtraídos
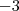
e

e o resultado fica

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Magda » Sex Ago 07, 2009 19:49
por Magda » Sex Ago 07, 2009 19:49
Grata por mais esta ajuda.
Magda
-
Magda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 19, 2009 18:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas
por Jansen » Dom Mai 10, 2009 00:01
- 5 Respostas
- 4694 Exibições
- Última mensagem por Molina

Seg Mai 11, 2009 04:36
Sistemas de Equações
-
- Sistemas...
por GABRIELA » Ter Set 08, 2009 21:41
- 6 Respostas
- 3479 Exibições
- Última mensagem por GABRIELA

Qua Set 09, 2009 18:52
Matrizes e Determinantes
-
- Sistemas
por GABRIELA » Qua Set 09, 2009 18:59
- 2 Respostas
- 1711 Exibições
- Última mensagem por GABRIELA

Qui Set 10, 2009 17:08
Sistemas de Equações
-
- Sistemas
por GABRIELA » Seg Set 21, 2009 17:25
- 4 Respostas
- 2398 Exibições
- Última mensagem por GABRIELA

Ter Set 22, 2009 09:45
Sistemas de Equações
-
- Sistemas
por Douglaspimentel » Qui Abr 15, 2010 18:39
- 1 Respostas
- 2417 Exibições
- Última mensagem por Elcioschin

Qui Abr 15, 2010 20:14
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\begin{cases}2(x+y)=x+3\rightarrow [2x+2y=x+3]\rightarrow [x+2y-3=0]\\y+3=3(x-y)\rightarrow [y+3=3x-3y]\rightarrow [3x-4y-3=0]\end{cases} \begin{cases}2(x+y)=x+3\rightarrow [2x+2y=x+3]\rightarrow [x+2y-3=0]\\y+3=3(x-y)\rightarrow [y+3=3x-3y]\rightarrow [3x-4y-3=0]\end{cases}](/latexrender/pictures/7bf3af84b1a3f536f31a399e345852e6.png)
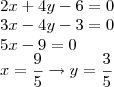
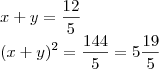







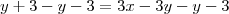
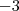 e
e  e o resultado fica
e o resultado fica 

 .
.
 :
: