 por mdroid » Dom Mar 25, 2012 16:04
por mdroid » Dom Mar 25, 2012 16:04
Boa tarde.
tenho o seguinte problema para resolver mas estou com dúvidas:
Problema: Verificar se é verdadeira a seguinte igualdade e justificar:

Após analisar, percebi que se fosse
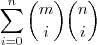
, (sem o

a multiplicar por

)
aplicando a lei da simetria dava

e aplicando a convolução de vandermonde

e depois continuava-se sem o somatório.
A minha pergunta é como eu lido com o

dentro do somatório de forma a validar a igualdade inicial? Pelas propriedades dos somatório que conheço, não é possível passar o

para fora do somatório.
Obrigado.
-
mdroid
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 25, 2012 15:41
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida sobre determinar a igualdade (3x-1)/(2x-6)<3
 por Xremix31 » Sáb Abr 09, 2022 16:27
por Xremix31 » Sáb Abr 09, 2022 16:27
- 1 Respostas
- 9013 Exibições
- Última mensagem por Sobreira

Dom Jun 19, 2022 19:00
Inequações
-
- Igualdade de números complexos - Duvida em exercicio
por DonTLie » Qui Mar 11, 2010 17:23
- 4 Respostas
- 16004 Exibições
- Última mensagem por MarceloFantini

Sex Mar 12, 2010 17:40
Tópicos sem Interação (leia as regras)
-
- Somatório
por ARCS » Sáb Mar 12, 2011 01:51
- 3 Respostas
- 4076 Exibições
- Última mensagem por Renato_RJ

Sáb Mar 12, 2011 03:14
Sequências
-
- Somatório
por Abelardo » Sex Abr 01, 2011 01:06
- 0 Respostas
- 1449 Exibições
- Última mensagem por Abelardo

Sex Abr 01, 2011 01:06
Álgebra Elementar
-
- Combinações
por Leone de Paula » Seg Mai 21, 2012 17:49
- 1 Respostas
- 2185 Exibições
- Última mensagem por DanielFerreira

Ter Mai 22, 2012 23:42
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

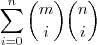 , (sem o
, (sem o  a multiplicar por
a multiplicar por  )
)
 e depois continuava-se sem o somatório.
e depois continuava-se sem o somatório. dentro do somatório de forma a validar a igualdade inicial? Pelas propriedades dos somatório que conheço, não é possível passar o
dentro do somatório de forma a validar a igualdade inicial? Pelas propriedades dos somatório que conheço, não é possível passar o  para fora do somatório.
para fora do somatório.

