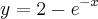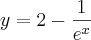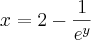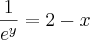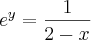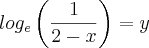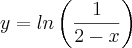por Rhyu » Sex Mar 23, 2012 21:23
por Rhyu » Sex Mar 23, 2012 21:23
Bom queria saber como resolver isso
f(x)= 2 - e^-x (e elevado a -x)
Encontre a função inversa de f(x)
Galera sempre fico em dúvida de como resolver exercicios em que existe a notação "e" alguém tem uma dica?
-
Rhyu
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 23, 2012 21:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por DanielFerreira » Sex Mar 23, 2012 22:50
por DanielFerreira » Sex Mar 23, 2012 22:50
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Rhyu » Sex Mar 23, 2012 22:54
por Rhyu » Sex Mar 23, 2012 22:54
danjr acho que é isso mesmo, tive um teste de calculo que uma das perguntas era essa, e não consegui resolver por causa da notação "e" fico perdido quando aparece isso não sei se tem que substituir por In ou log e . Se tem alguma dica?
-
Rhyu
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 23, 2012 21:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por DanielFerreira » Sex Mar 23, 2012 23:18
por DanielFerreira » Sex Mar 23, 2012 23:18
Rhyu escreveu:danjr acho que é isso mesmo, tive um teste de calculo que uma das perguntas era essa, e não consegui resolver por causa da notação "e" fico perdido quando aparece isso não sei se tem que substituir por In ou log e . Se tem alguma dica?
Rhyu,
você poderá usar qualquer das duas, mas em Cálculo é comum
ln.
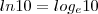
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3397 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2642 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7723 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1183 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2207 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



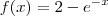
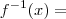 ?
?