 por rareirin » Qua Fev 22, 2012 17:07
por rareirin » Qua Fev 22, 2012 17:07
Aparenta ser um exercício simples, queria uma explicação bem detalhada se possível. Obrigado

-
rareirin
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Fev 22, 2012 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por joaofonseca » Qua Fev 22, 2012 17:28
por joaofonseca » Qua Fev 22, 2012 17:28
Antes de dar algumas pistas para a resolução deste problema.Não resisto a perguntar.
rareirin estás mesmo a frequentar o curso de engenharia civil, conforme consta no teu perfil???
Se substituir-mos
x por 1 chegamos a uma indeterminação do tipo 0/0.Portanto temos de decompor denominador e numerador para eleminar o fator comum.
No numerador, deves primeiro colocar em evidência o 3, de forma a evitar o coeficiênte de

maior que 1.Depois é decompor seja o numerador, seja o denominador, mantendo sempre o 3 em evidência.
O monomio [tex]x-1[/text] será o fator comum, e assim pode ser eliminado tanto do denominador como do numerador.
A partir daqui basta substituir
x por 1, não esquecendo de multiplicar por 3.No fim basta simplificar a fração.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por rareirin » Qui Fev 23, 2012 10:17
por rareirin » Qui Fev 23, 2012 10:17
Na verdade hoje é o primeiro dia de aula. KKK
Quero entrar sabendo alguma coisa, costume meu =)
-----------------------------------------------------------------
Nossa não conseguir entender nada

Acho melhor eu ir nas aulas para depois tirar minha dúvidas

-
rareirin
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Fev 22, 2012 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Fev 23, 2012 13:10
por LuizAquino » Qui Fev 23, 2012 13:10
rareirin escreveu:Na verdade hoje é o primeiro dia de aula. KKK
Quero entrar sabendo alguma coisa, costume meu =)
-----------------------------------------------------------------
Nossa não conseguir entender nada

Acho melhor eu ir nas aulas para depois tirar minha dúvidas

Eu gostaria de recomendar que você assista a videoaula "01. Cálculo I - Noção Intuitiva de Limite". Ela está disponível em meu canal no YouTube:
http://www.youytube.com/LCMAquinoApós assistir a videoaula, tente resolver esse exercício.
DicaPara resolver o limite que você deseja, primeiro você precisa fatorar os polinômios que aparecem na fração. Em seguida, basta efetuar uma simplificação.
Vale lembrar que uma expressão polinomial do 2º grau dada por

pode ser escrita na sua forma fatorada como sendo
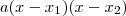
, onde

e

são as raízes da equação

. Em outras palavras, temos que:
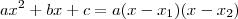
.
ExemploConsidere a expressão polinomial do 2º grau dada por
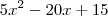
.
Calculando as raízes da equação

, obtemos

e

. Portanto, a forma fatorada desse polinômio é:

Confira essa relação. Aplique a distributiva para desenvolver
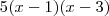
e verificar que o resultado será
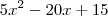
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6644 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4790 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5119 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7259 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4436 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 maior que 1.Depois é decompor seja o numerador, seja o denominador, mantendo sempre o 3 em evidência.
maior que 1.Depois é decompor seja o numerador, seja o denominador, mantendo sempre o 3 em evidência.




 pode ser escrita na sua forma fatorada como sendo
pode ser escrita na sua forma fatorada como sendo 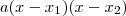 , onde
, onde  e
e  são as raízes da equação
são as raízes da equação  . Em outras palavras, temos que:
. Em outras palavras, temos que: 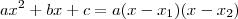 .
.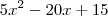 .
. , obtemos
, obtemos  e
e  . Portanto, a forma fatorada desse polinômio é:
. Portanto, a forma fatorada desse polinômio é:
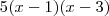 e verificar que o resultado será
e verificar que o resultado será 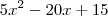 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.