


 maior que 1.Depois é decompor seja o numerador, seja o denominador, mantendo sempre o 3 em evidência.
maior que 1.Depois é decompor seja o numerador, seja o denominador, mantendo sempre o 3 em evidência.



rareirin escreveu:Na verdade hoje é o primeiro dia de aula. KKK
Quero entrar sabendo alguma coisa, costume meu =)
-----------------------------------------------------------------
Nossa não conseguir entender nada
Acho melhor eu ir nas aulas para depois tirar minha dúvidas
 pode ser escrita na sua forma fatorada como sendo
pode ser escrita na sua forma fatorada como sendo 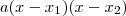 , onde
, onde  e
e  são as raízes da equação
são as raízes da equação  . Em outras palavras, temos que:
. Em outras palavras, temos que: 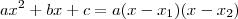 .
.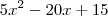 .
. , obtemos
, obtemos  e
e  . Portanto, a forma fatorada desse polinômio é:
. Portanto, a forma fatorada desse polinômio é:
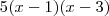 e verificar que o resultado será
e verificar que o resultado será 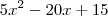 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
