Tenho uma duvida que me esta a impedir de continuar a estudar . Num exercicio de estimação , metodo dos momentos , aparece-me uma funçao com modulo e nao sei como resolvê-la.
Uma amostra casual de dimensao n=5 tem como funçao
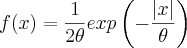e sabendo que 
tem distribuição exponencial de parametro 
obter o estimador dos momentos para .Tentei faze-lo , mas nao consegui acabando por resolver pelo metodo da maxima verosimilhança dando
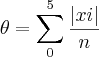, mas penso que pelo outro metodo é diferente e nao sei como faze-lo.Alguem me consegue ajudar ?
Obrigada
.
