


Camila Z escreveu:Bom, preciso provar que:
Boa noite Camila Z.
(senx+cosx)(senx-cosx)=2sen^2x -1

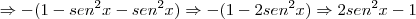

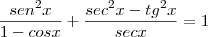 ?
?


Camila Z escreveu:Obrigada, mas eu tenho que detalhar "provando" que dá o quadrado do 1º menos o quadrado do 2º... me ajude
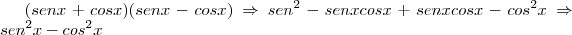 (Diferença de quadrados!)
(Diferença de quadrados!)Camila Z escreveu:A segunda é isso mesmo... como fica?
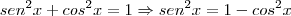
 então
então 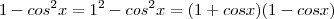 //
//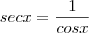 //
// //
//




Camila Z escreveu:Muito obrigada mesmo, mas vendo o detalhamento da 2ª, eu queria enviar o meu desenvolvimento para vc dar uma olhada... é muito para digitar, como faço para enviar como figura? O meu fica com 1 cosx no final...
Camila Z escreveu:Ah, gente, desculpa, recebi uma mensagem de que pode estar errado o sinal de + no meio das frações, parece que é -! Ai sim fica ok, né?



Camila Z escreveu:


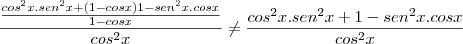
 não está em ambos os lados da soma.
não está em ambos os lados da soma.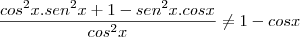
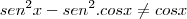









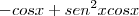 do denominador, é necessário você colocá-lo em evidência tanto no numerador quanto no denominador.
do denominador, é necessário você colocá-lo em evidência tanto no numerador quanto no denominador.




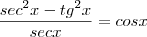



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)