


highway escreveu:Pela definição de limite, encontre a equação da reta tangente á curva Y=2x²-1 no ponto de abcissa 1.
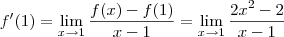
 . Eu recomendo que você tente encontrar esse resultado.
. Eu recomendo que você tente encontrar esse resultado.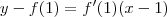

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.
 :
: