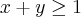[Help]Problemas de Análise Matemática 2

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Help]Problemas de Análise Matemática 2

Regras do fórum
Responder

[Help]Problemas de Análise Matemática 2

Mensagempor Saturnino Nataniel » Seg Dez 12, 2011 20:05

Boa Noite pessoal! Bom Sou o Nataniel sou angolano e tenho 17anos de idade estudante de Engenharia do 1º ano!
Nunca participei de forums de Matemática, apenas de Informática, mais especificamente na área de informática...
Gostaria que alguem de boa fé me ajudasse na resolução desses 2 de 4 exercícios...
http://i.imgur.com/twj66.jpg
http://i.imgur.com/twj66.jpg
Grato pela atenção!
Saturnino Nataniel
Novo Usuário
Novo Usuário
 
Mensagens: 4
Registrado em: Ter Jul 12, 2011 17:34
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Informática
Andamento: cursando
Voltar ao topo

Re: [Help]Problemas de Análise Matemática 2

Mensagempor LuizAquino » Qua Dez 14, 2011 09:00

Saturnino Nataniel escreveu:Boa Noite pessoal! Bom Sou o Nataniel sou angolano e tenho 17anos de idade estudante de Engenharia do 1º ano!
Nunca participei de forums de Matemática, apenas de Informática, mais especificamente na área de informática...
Gostaria que alguem de boa fé me ajudasse na resolução desses 2 de 4 exercícios...
http://i.imgur.com/twj66.jpg
http://i.imgur.com/twj66.jpg
Grato pela atenção!


Por favor, por questão de organização do fórum, escreva aqui todo o texto do exercício, enviando como imagem apenas o que for necessário.

Aproveito para frisar que enviar o texto do exercício como uma imagem prejudica o sistema de busca do fórum.
professoraquino.com.br | youtube.com/LCMAquino | @lcmaquino

"Sem esforço, não há ganho."
Dito popular.
Avatar do usuário
LuizAquino
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 2654
Registrado em: Sex Jan 21, 2011 09:11
Localização: Teófilo Otoni - MG
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Mestrado - Modelagem Computacional
Andamento: formado
Voltar ao topo

Re: [Help]Problemas de Análise Matemática 2

Mensagempor Saturnino Nataniel » Sáb Dez 17, 2011 14:49

Desculpa aí mano! Não voltará a acontecer!
Fiz uma prova de Análise Matemática II, mas acho que fui injustiçado na correcção, 2ª feira terei um debate com o professor gostaria que alguem confirmasse se o meu resultado está certo, por favor!
A questã é a seguinte:
"Calcule o momento de inércia em relação à origem de uma placa uniforme, de massa M e tal que {y}^2{}+{x}^{2}\leq 1^0 \leq x \leq y^x + y \geq 1
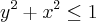
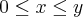
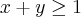
Meu resultado foi: I= 0
gostaria que alguem confirmasse o resultado por favor!
OBS: Não consegui escrever a conjunção "e" (^) tive que improvisar, ficou muito pequeno!
Saturnino Nataniel
Novo Usuário
Novo Usuário
 
Mensagens: 4
Registrado em: Ter Jul 12, 2011 17:34
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Informática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

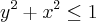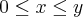Índice do fórum