Boa Noite pessoal! Bom Sou o Nataniel sou angolano e tenho 17anos de idade estudante de Engenharia do 1º ano!
Nunca participei de forums de Matemática, apenas de Informática, mais especificamente na área de informática...
Gostaria que alguem de boa fé me ajudasse na resolução desses 2 de 4 exercícios...
http://i.imgur.com/twj66.jpg
http://i.imgur.com/twj66.jpg
Grato pela atenção!



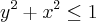 ^
^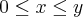 ^
^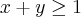
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)