Grafico Derivada

[luanalcs]

Pessoal

Estou tendo dificuldades para esboçar o gráfico da função a seguir:

f(x)=2x³+x-2

1º Passo: Derivada
f'(x)=6x²+1

2º Passo: Pontos críticos (mínimos e máximos)
f'(x)=0
6x²+1=0
6x²=-1
x²=-1/6
x=+-1/6

3º Passo: Determinar pontos críticos
x= 1/6
f(x)=2x³+x-2
2*(0,1666)³+(0,1666)-2= 7 (1/6,7)

x= (-1/6)
f(x)=2x³+x-2
2*(-0,1666)³+(-0,1666)-2= -11 (1/6,-11)

4º Passo: Segunda derivada da função
f(x)=6x²+1
f"(x)=12x

5º Passo: Definir concavidade no ponto crítico
x= 1/6
f"(1/6)=12*1/6= 2 (Para cima)

x= -1/6
f"(-1/6)=12*(-1/6)= -2 (Para baixo)

6º Passo: Ponto de inflexão
f"(x)=0
12x=0
x=0

f(x)=2x³+x-2
f(0)= 2*0³+0-2= -2

Creio que esteja errada a montagem do gráfico, marquei (-1/6,-11) (1/6,7) (0,2).

Não consigo vizualizar aonde possa estar o erro.

Desde já agradeço

[joaofonseca]

O erro está nos zeros da derivada.



Não tem zeros reais.O vertice da parabola será um minimo.Com alguma atenção se verifica que a função pode ser escrita da seguite forma: em que 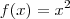. Podemos concluir que o vertice da função elementar sofreu uma deslocação de 1 unidade para cima.Assim de (0,0) passou para (0,1). O fator de expanção 6, não afeta em nada o vertice da parabola.
Concluimos que se o minimo da parabola é (0,1) então não há zeros.Se a derivada não tem zeros e é positiva em todo o seu dominio, f(x) é estritamente crescente.

Todos os calculos posteriores que utilizam as falsas raizes da derivada estam errados.
Aqui fica uma fotografia:

derivadas.jpg (15.1 KiB) Exibido 1509 vezes

[LuizAquino]

Olá joaofonseca e luanalcs,

Já que a dúvida foi resolvida, gostaria apenas de deixar uma sugestão. Trata-se do programa GeoGebra, que com certeza pode ajudar muito nos seus estudos.

A página oficial desse programa é:
http://www.geogebra.org

Se vocês desejarem, no meu canal no YouTube tem um conjunto de tutoriais sobre esse programa. O endereço é:
http://www.youtube.com/LCMAquino

Em particular, eu recomendo o vídeo tutorial "10. Curso de GeoGebra - Funções".

Por fim, se vocês precisarem fazer uma revisão, no meu canal também há uma vídeo-aula tratando sobre a construção de gráficos: "22. Cálculo I - Construção de Gráficos".