 por markdsp » Qua Out 19, 2011 09:18
por markdsp » Qua Out 19, 2011 09:18
Gostaria de uma ajuda pra fazer uma montagem de preço. exemplo: tenho custo 100 reais de um produto. preco aplicar a ele 20% de taxa de comissao. se eu fizer o calculo de 100,00+20% daria o resultado de 120 reais. entretanto, quando eu fosse fazer o calculo tirando de 20% de 120, é claro que nao daria mais os 120 e sim 96 reais. nesse caso iria comer dentro do custo.
queria saber se existe uma formula em que eu possa aplicar sobre o valor de custo em que no final eu possa descontar o percentual de comissao e nesse nao reduza o valor de custo do produto, sem que pra isso eu de tanta volta de calculo.
fazendo aqui por estimativa, achei o calculo de somar ao custo o percentual de 25% para no final do valor de venda poder descontar os 20% e encontrar o valor final do custo e assim fechar as contas. exemplo: 100,00 +25% = 125,00(preço de venda) fazendo o desconto reverso.... 125,00 -20%(taxa que preciso tirar no final)= 100,00 preco final de custo original.
mas percebo q este calculo nao e uma formula e sim uma saida que podera em alguns casos nao dar certo. por isso preciso de uma formula logica pra fazer essa conta e aplicar sobre o custo para chegar a um valor de venda final de forma que quando eu for descontar percentual de comissão eu tenha no final o valor final de custo original.
podem me ajudar?
-
markdsp
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 19, 2011 08:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: gestao
- Andamento: cursando
 por Neperiano » Qua Out 19, 2011 18:44
por Neperiano » Qua Out 19, 2011 18:44
Ola
Qual o custo de um produto vendido a 120 reais, sabendo que 20% é taxa de comissão qual o preço do produto tirando a comissão
120 = 120%
x = 100%
x=100 reais
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por markdsp » Qui Out 20, 2011 19:44
por markdsp » Qui Out 20, 2011 19:44
Neperiano escreveu:Ola
Qual o custo de um produto vendido a 120 reais, sabendo que 20% é taxa de comissão qual o preço do produto tirando a comissão
120 = 120%
x = 100%
x=100 reais
Atenciosamente
Obrigado pela contribuição.
nao tinha pensado dessa forma. entretanto, pense sob a otica de um vendedor que ganha por comissionamento. o calculo nao seria feito colocando os 120 que é o preco final que ele vende, calculando valendo 120% tb. nesse caso o processo seria o calculo de 120 = 100% e dai se tira os 20% dele. que seria no final os 96 reais.
nesse caso eu gostaria de saber se existe uma formula pra que eu pudesse calcular o preco, somando o meu custo mais o percentual de comissao e nesse desse um resultado final que quando fosse fazer reversamente apurasse exatamente o valor que devo pagar de comissao sobrando enfim exatamente o meu custo. ou seja. no final de descontado o percentual de 20% sobrasse ainda os 100 reais e nao 96 reais. consegui explicar melhor ?
agradeco a contribuicao que puder ajudar!
-
markdsp
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 19, 2011 08:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: gestao
- Andamento: cursando
 por Neperiano » Sex Out 21, 2011 14:02
por Neperiano » Sex Out 21, 2011 14:02
Ola
Vou tentar mostra fazendo um outro exercício que eu invetei agora
O custo de um determinado produto é 50 reais e que a loja vende a lucro 0, calcule o seu preço sabendo que a comissão do vendedor é 5% sobre o preço de venda?
50 - 100%
x - 105%
x = 52,5 esse é o preço de venda
Agora vejamos, sabendo que o preço de venda de determinado produto é 52,5 reais, determine seu custo se a comissão do vendedor sobre o preço de venda é 5% e se o lucro da loja é 0?
52,5 - 105
x - 100
x = 50
Não tem fórmula, faça regra de três, o segredo é somar os 5% da comissão nos 100% total, sempre faça isso com a comissão, você torna o custo como 100% e não o preço de venda.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por mausim » Qui Out 27, 2011 09:13
por mausim » Qui Out 27, 2011 09:13
markdsp escreveu:Gostaria de uma ajuda pra fazer uma montagem de preço. exemplo: tenho custo 100 reais de um produto. preco aplicar a ele 20% de taxa de comissao. se eu fizer o calculo de 100,00+20% daria o resultado de 120 reais. entretanto, quando eu fosse fazer o calculo tirando de 20% de 120, é claro que nao daria mais os 120 e sim 96 reais. nesse caso iria comer dentro do custo.
queria saber se existe uma formula em que eu possa aplicar sobre o valor de custo em que no final eu possa descontar o percentual de comissao e nesse nao reduza o valor de custo do produto, sem que pra isso eu de tanta volta de calculo.
fazendo aqui por estimativa, achei o calculo de somar ao custo o percentual de 25% para no final do valor de venda poder descontar os 20% e encontrar o valor final do custo e assim fechar as contas. exemplo: 100,00 +25% = 125,00(preço de venda) fazendo o desconto reverso.... 125,00 -20%(taxa que preciso tirar no final)= 100,00 preco final de custo original.
mas percebo q este calculo nao e uma formula e sim uma saida que podera em alguns casos nao dar certo. por isso preciso de uma formula logica pra fazer essa conta e aplicar sobre o custo para chegar a um valor de venda final de forma que quando eu for descontar percentual de comissão eu tenha no final o valor final de custo original.
podem me ajudar?
Se entendi bem, sua necessidade é calcular um valor de venda que, retirando-se 20% dele, dê o valor de custo.
Se é assim, chamando de 'p' o valor de venda, de 'c' o valor de custo e de 't' a taxa de comissão (taxa unitária), teríamos

Isto é: do meu preço de venda, retiro uma parte dele mesmo (a comissão), que deve sobrar exatamente o preço de custo.
Continuando,

Assim,
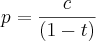
No exemplo de o preço de custo ser 100,00 e a taxa de comissão 20%, teríamos o preço de venda

-
mausim
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Out 25, 2011 10:27
- Formação Escolar: SUPLETIVO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lei da formaçao
por brunoscollaro » Sáb Out 22, 2011 11:29
- 4 Respostas
- 3178 Exibições
- Última mensagem por MarceloFantini

Sáb Out 22, 2011 17:38
Funções
-
- FORMAÇÃO DE PREÇO
por rasecmussel » Qua Jan 18, 2012 21:43
- 1 Respostas
- 1522 Exibições
- Última mensagem por DanielFerreira

Ter Fev 21, 2012 17:48
Álgebra Elementar
-
- Formação de triângulo no plano cartesiano
por Jonatan » Sex Jul 23, 2010 10:56
- 0 Respostas
- 1530 Exibições
- Última mensagem por Jonatan

Sex Jul 23, 2010 10:56
Geometria Analítica
-
- Analise Cobinatoria - Posibilidades de formação de nºs
por ReDeDeR » Sex Abr 13, 2012 23:54
- 3 Respostas
- 4994 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 14, 2012 20:03
Estatística
-
- [Descoberta da lei de formação...] Se refere a que matéria?
por cavalcantebry » Sex Out 12, 2012 16:58
- 4 Respostas
- 3404 Exibições
- Última mensagem por cavalcantebry

Sáb Out 13, 2012 15:40
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





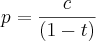


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.