
e chego sempre nessa parte:
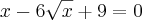
tem como melhorar essa expressão?
Bom dia!
Obrigado!


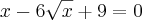

![\lim_{x\rightarrow9}\frac{\sqrt[]{x}-3}{x-9} \lim_{x\rightarrow9}\frac{\sqrt[]{x}-3}{x-9}](/latexrender/pictures/0324429348c96bbd301924d99fadabdd.png) e só fazer o conjugado em cima em baixo de assim :
e só fazer o conjugado em cima em baixo de assim :![\lim_{x\rightarrow9}\frac{\sqrt[]{x}-3}{x-9}*\frac{\sqrt[]{x}+3}{\sqrt[]{x}+3} \lim_{x\rightarrow9}\frac{\sqrt[]{x}-3}{x-9}*\frac{\sqrt[]{x}+3}{\sqrt[]{x}+3}](/latexrender/pictures/8a0718097d60050556969e4c0766ef02.png) dessa forma multiplicando e dividindo pelo mesmo conjudado eu não altero a fração. Depois do conjugado fica assim:
dessa forma multiplicando e dividindo pelo mesmo conjudado eu não altero a fração. Depois do conjugado fica assim:![\lim_{x\rightarrow9}\frac{{(\sqrt[]{x})}^{2}-{(3)}^{2}}{(x-9)(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{{(\sqrt[]{x})}^{2}-{(3)}^{2}}{(x-9)(\sqrt[]{x}+3)}](/latexrender/pictures/a42ecb8a5baa1c9d35d77c848d62f960.png) agora tente resolver e quaquer duvida o pessoal está ai a disposição.
agora tente resolver e quaquer duvida o pessoal está ai a disposição. 


![\lim_{x\rightarrow9}\frac{{(\sqrt[]{x})}^{2}-({3})^{2}}{(x-9)(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{{(\sqrt[]{x})}^{2}-({3})^{2}}{(x-9)(\sqrt[]{x}+3)}](/latexrender/pictures/9caf6df522f74e6d16efaed05b5e592c.png)
![{(\sqrt[]{2})}^{2} {(\sqrt[]{2})}^{2}](/latexrender/pictures/bf61b10c2788127e9d6394e37b7eea18.png) eu posso simplificar o esposnte dois pela raiz que no caso o indece é dois. Lembrando que o indece dois não precisamos representa-lo ok? tranquilo!
eu posso simplificar o esposnte dois pela raiz que no caso o indece é dois. Lembrando que o indece dois não precisamos representa-lo ok? tranquilo!  . Bom nesse caso podemos tabém cortar a raiz com o indice assim :
. Bom nesse caso podemos tabém cortar a raiz com o indice assim : ![{(\sqrt[]{x})}^{2} {(\sqrt[]{x})}^{2}](/latexrender/pictures/cd669de06ee6c6d7d3d1e5d68870d631.png) e é posivel cortar o indice com o espoente 2 do x ficando assim :
e é posivel cortar o indice com o espoente 2 do x ficando assim :![{(\sqrt[]{x})}^{2}=x {(\sqrt[]{x})}^{2}=x](/latexrender/pictures/41c114c2f19108c7af33f513a483ff9b.png) e o 3 elevado a 2 é 9 porque 3.3=9 beleza?
e o 3 elevado a 2 é 9 porque 3.3=9 beleza?  . Depois de Você fizer, o limite fica assim :
. Depois de Você fizer, o limite fica assim :![\lim_{x\rightarrow9}\frac{(x-9)}{(x-9)(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{(x-9)}{(x-9)(\sqrt[]{x}+3)}](/latexrender/pictures/9a4be705d2e05960671ea8e34a684857.png) ai se você prestou atenção veja que o x-9 tanto em cima como em baixo tende a 0 por que? se eu substituir e resolver continua a dar a indeterminação 0/0. então o que fazer ? basta simplificar o x-9 em cima em baixao, ou seja corta em cima e em baixo pois são termos semelhante. Lembrando que isso só pode ser feito pois o x tende a 9, x não é 9 , se fosse 9 eu teria uma simplificação invalida . Obs : Valeww Luiz Alquino pelas suas video-aula de limite. Voltando você deve simplificar o x-9 o que vai dar esse limite equivalente:
ai se você prestou atenção veja que o x-9 tanto em cima como em baixo tende a 0 por que? se eu substituir e resolver continua a dar a indeterminação 0/0. então o que fazer ? basta simplificar o x-9 em cima em baixao, ou seja corta em cima e em baixo pois são termos semelhante. Lembrando que isso só pode ser feito pois o x tende a 9, x não é 9 , se fosse 9 eu teria uma simplificação invalida . Obs : Valeww Luiz Alquino pelas suas video-aula de limite. Voltando você deve simplificar o x-9 o que vai dar esse limite equivalente:![\lim_{x\rightarrow9}\frac{(x-9)}{(x-9)(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{(x-9)}{(x-9)(\sqrt[]{x}+3)}](/latexrender/pictures/9a4be705d2e05960671ea8e34a684857.png) =
=![\lim_{x\rightarrow9}\frac{1}{(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{1}{(\sqrt[]{x}+3)}](/latexrender/pictures/c78533a5d367b9aa62410f068ef32c51.png) , problema resolvido , agora é só substituir pelo valor que ele esta tendendo que nesse caso é 9, então temos : >>>>>>>>>
, problema resolvido , agora é só substituir pelo valor que ele esta tendendo que nesse caso é 9, então temos : >>>>>>>>>![\lim_{x\rightarrow9}\frac{1}{(\sqrt[]{x}+3)} \lim_{x\rightarrow9}\frac{1}{(\sqrt[]{x}+3)}](/latexrender/pictures/c78533a5d367b9aa62410f068ef32c51.png) =
=![\lim_{x\rightarrow9}\frac{1}{(\sqrt[]{9}+3)} \lim_{x\rightarrow9}\frac{1}{(\sqrt[]{9}+3)}](/latexrender/pictures/a25efc19cf41e5d239b7adb9439e2f4a.png) raiz de 9 é 3 porque 3.3 duas vezes é 9. continuando ......>>>>>>>
raiz de 9 é 3 porque 3.3 duas vezes é 9. continuando ......>>>>>>> espero que tenha comprendido essa bagunça que eu fiz rsrsrsr
espero que tenha comprendido essa bagunça que eu fiz rsrsrsr  ! faloww amigo.
! faloww amigo.



![x-9=(\sqrt[]{x}-3)(\sqrt[]{x}+3) x-9=(\sqrt[]{x}-3)(\sqrt[]{x}+3)](/latexrender/pictures/75e55a11300c4a135ff612ea761863fc.png) ---> Diferença de dois quadrados
---> Diferença de dois quadrados![\lim_{x\rightarrow{9}}\frac{\sqrt[]{x}-3}{x-9}\Rightarrow \lim_{x\rightarrow{9}}\frac{(\sqrt[]{x}-3)}{(\sqrt[]{x}-3)(\sqrt[]{x}+3)}\Rightarrow \lim_{x\rightarrow{9}}\frac{1}{\sqrt[]{9}+3}= \frac{1}{6} \lim_{x\rightarrow{9}}\frac{\sqrt[]{x}-3}{x-9}\Rightarrow \lim_{x\rightarrow{9}}\frac{(\sqrt[]{x}-3)}{(\sqrt[]{x}-3)(\sqrt[]{x}+3)}\Rightarrow \lim_{x\rightarrow{9}}\frac{1}{\sqrt[]{9}+3}= \frac{1}{6}](/latexrender/pictures/3e2e985ee19a902ae42f4b6e0a3c7734.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.