a)determine a lei que define a função
b)calcule a área da região compreendida entre os gráficos de f e
, o eixo dos y e a reta de equação x=1Por favor se puderem explicar passo-a - passo, detalhadamente, agradeço!
por felipy » Sex Set 02, 2011 23:38
, o eixo dos y e a reta de equação x=1
por Neperiano » Sáb Set 03, 2011 11:58
eu acho que seria inverter ela, ou seja como tu faz a função de
é 
certo né, acho que é a mesma coisa.
por felipy » Sáb Set 03, 2011 12:39
por Neperiano » Sáb Set 03, 2011 14:32
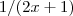e dai na b, voce faz a integral da maior no gráfico menos a menorpor MarceloFantini » Sáb Set 03, 2011 15:51
e não ![[f(x)]^{-1}](/latexrender/pictures/5965afd864edd417f09c34550b621617.png "[f(x)]^{-1}")
. Para encontrar a função inversa devemos encontrar x em função de y: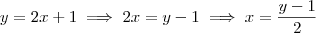
, logo 
.
por felipy » Sáb Set 03, 2011 22:43
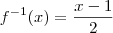MarceloFantini escreveu:Neperiano, você continua se confundindo com a notação. A questão quer dizer a função inversa, denotada por
Agora para o item b desenhe a região e calcule sua área. Parece questão de vestibular, então imagino que integrar não será necessário, provavelmente é possível encontrar esta área por formas elementares.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a e elevar ao quadrado os dois lados)