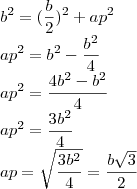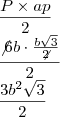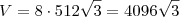![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) cm³.
cm³.Resolução:
Por se tratar de um prisma hexagonal sua base é composta de 6 triângulos equiláteros. Dessa forma, a área lateral é 6 vezes a área de um retângulo (base x altura) resultando em 48b (6.b.8) e a área da base é
![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png) .
.Assim, é substituído tanto a área da base quanto a área lateral na fórmula da área total. Lembrando que a área total é igual 3 vezes a área lateral.
Atotal = Alateral + 2.Abase
3.48b = 48b + 2.
![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png)
144b = 48b +
![\frac{6{l}^{2}\sqrt[]{3}}{2} \frac{6{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/a5881b8200c33cb85e02f7b13964d548.png) -> simplificando fica
-> simplificando fica ![\frac{3{l}^{2}\sqrt[]{3}}{1} \frac{3{l}^{2}\sqrt[]{3}}{1}](/latexrender/pictures/92cc86d90b45efd42c314c0316cc3256.png)
144b - 48b =
![\frac{3{l}^{2}\sqrt[]{3}}{1} \frac{3{l}^{2}\sqrt[]{3}}{1}](/latexrender/pictures/92cc86d90b45efd42c314c0316cc3256.png)
b =
![\frac{3{l}^{2}\sqrt[]{3}}{96} \frac{3{l}^{2}\sqrt[]{3}}{96}](/latexrender/pictures/5b9d523c308a5462fdb12d8dc76259ee.png)
b =
![\frac{{l}^{2}\sqrt[]{3}}{32} \frac{{l}^{2}\sqrt[]{3}}{32}](/latexrender/pictures/63bd1fc232f56d9d2fc1af2a995bc4c1.png) cm
cmApós encontrar o valor de b, substitui-se o valor de "b" na área lateral:
Alateral = 48b
Alateral =
![48.\frac{{l}^{2}\sqrt[]{3}}{32} 48.\frac{{l}^{2}\sqrt[]{3}}{32}](/latexrender/pictures/2e18e3ca32376bef5184920cd5b4309c.png)
Alateral =
![\frac{48{l}^{2}\sqrt[]{3}}{32} \frac{48{l}^{2}\sqrt[]{3}}{32}](/latexrender/pictures/38dd630e1da8264820346d469096576c.png) -> simplificando fica igual à...
-> simplificando fica igual à...Alateral =
![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png) cm²
cm²Isso mostra que a área lateral desse hexágono é igual a área da base do mesmo.
Para encontrar o valor de "l" iguala-se a área da base, à área lateral.
![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png) =
= ![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png) -> simplifica 2 com 2 e 3 com 3.
-> simplifica 2 com 2 e 3 com 3.l² =
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
l =
![\sqrt[]{\sqrt[]{3}} \sqrt[]{\sqrt[]{3}}](/latexrender/pictures/de34b711b210814bb0ddd1f984ac8c4b.png) -> simplifica os radicais.
-> simplifica os radicais.l = 3 cm
Agora substitui o valor de "l" na fórmula do volume:
V = Abase.h
V =
![\frac{3{l}^{2}\sqrt[]{3}}{2} \frac{3{l}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/03518d511755e956791b5220eed156b3.png) .8
.8V =
![\frac{3.{3}^{2}\sqrt[]{3}}{2} \frac{3.{3}^{2}\sqrt[]{3}}{2}](/latexrender/pictures/72a635ae0a33274f9578b9cb88bac6f1.png) .8
.8V =
![\frac{3.9\sqrt[]{3}}{2} \frac{3.9\sqrt[]{3}}{2}](/latexrender/pictures/8f93bd583ae0359a771f44d38ba1fa3a.png) .8
.8V =
![\frac{27\sqrt[]{3}}{2} \frac{27\sqrt[]{3}}{2}](/latexrender/pictures/488bc12317aa5f7100c0e3a8661fd810.png) .8
.8V =
![\frac{216\sqrt[]{3}}{2} \frac{216\sqrt[]{3}}{2}](/latexrender/pictures/a47c2b0472037a8f88a32ed691f332c4.png)
V = 108
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) cm³
cm³Já refiz várias vezes e sempre encontro esse valor. Não sei onde errei ou se o gabarito está errado. Preciso de ajuda com esse exercício, por favor!
Obrigada e parabéns pelo forúm!