Bom dia! Começei a pouco estudar para um concurso, e surgiu um problema, que tive dificuldades para resolver (é simples pra muitos, mas estou meio enferrujado), consegui chegar ao resultado correto.
A cada 200m de distância da superficie terrestre, a temperatura cai 1 grau. Se na superficie a esta a +20 graus, qual a temperatura a 10km de distância?
Igualando as medidas... 10km x 1000 = 10000m
200m --------------1º
10000m---------------x
200x = 10000
x = 10000/200 = 50
ou seja, em 10000m vai cair a temperatura em 50º
+20 -50 = -30
Eu lembro na faculdade, que o professor para esses problemas montava uma tabela e chegava a uma formula, mas eu não lembro. Sabem que tipo de formula é? se sim poderiam me explicar? e me dizer se essa maneira que fiz foi a melhor forma de resolver?
Obrigado!


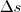 e variação de temperatura =
e variação de temperatura =  . Lembrando que uma função do primeiro grau é toda função do tipo
. Lembrando que uma função do primeiro grau é toda função do tipo 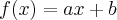 , onde
, onde  e
e  são números reais e
são números reais e  .
. 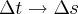


 e
e  . Colocando esses valores em
. Colocando esses valores em 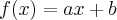 , teremos a seguinte lei:
, teremos a seguinte lei: 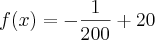 . Para comprovar a veracidade substitua procure ver qual é o valor de y quando o de for 10 Km.
. Para comprovar a veracidade substitua procure ver qual é o valor de y quando o de for 10 Km.

 .
.
 :
: