Boa tarde, Lunn.
Primeiramente parabéns pelo desenho. Fiz questão de utilizá-lo para explicar como você deve continuar sua questão.

Coloque essas letras
a, b, x da forma que estão para encontrarmos seus valores. Perceba que temos dois triângulos retângulos então podemos usar com facilidade seno, cosseno e tangente, caso necessite.
Pela informação do enunciado, temos que:
 (isto vai ser útil depois)
(isto vai ser útil depois)No triângulo da esquerda, temos que:
 (equação 1)
(equação 1)No triângulo da direita, temos que:
 (equação 2)
(equação 2)Perceba que as equações 1 e 2 possuem
x no seu lado direito. Assim, podemos igualá-los:

E daquela parte que eu falei que ia ser útil, fazemos a seguinte substituição:
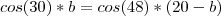
Resolvendo esta equação você encontrará o valor de
b e automaticamente o valor de
a.
Substitua estes valores nos triângulos e escolha um dos triângulos para trabalhar. Fazendo novamente o cosseno de um deles você irá descobrir o valor de
x e multiplicando por 2 este valor encontrará a distância entre os prédios.
Qualquer dúvida informe!