No colegiado desportivo foi realizada uma sessão em que foi votada a cassação do juiz Reginaldo. O Colegiado divide-se em
dois grandes grupos: o dos amigos de Reginaldo com elementos e o dos inimigos de Reginaldo com elementos. Reginaldo
somente será cassado se do colegiado votar pela sua cassação. Sabe-se que 25%dos amigos de Reginaldo
irão traí-lo e que 10% dos seus inimigos receberão uma gratificação para votar a seu favor. Reginaldo, também, sabe que, se todos os seus amigos votarem a seu favor, precisará de 40 votos de inimigos para não ser cassado.(Determine
quantos inimigosReginaldo possui, sabendo que ele escapou da cassação por 35 votos.
amigos(x) ----->a favor da cassação 25% de x = 1/4 de x
----->contra a cassação 75% de x = 3/4 de x
Inimigos(y) ------->contra cassação 10% de y = 1/10 de x
-------->a favor da cassação
xpara não ser cassado :
X+40 =
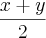
Determine
quantos inimigosReginaldo possui, sabendo que ele escapou da cassação por 35 votos.
a partir daí eu não consegui fazer
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.