 por clovis22 » Sex Jan 14, 2011 14:28
por clovis22 » Sex Jan 14, 2011 14:28
Olá! Tentei resolver uma questão, mas, por mais que tentasse, não consegui. Vou expô-la e depois mostrar como tentei resolvê-la:
(Fatec-SP) Em uma indústria há duas máquinas que funcionam em velocidades constantes, mas distintas entre si. Funcionando ininterruptamente, juntas, produzem X peças iguais em 2 horas e 40 minutos. Uma delas, sozinha, produziria essas peças em 4 horas de funcionamento ininterrupto. A outra produziria as X peças funcionando ininterruptamente em:
a) 8 horas e 15 minutos
b) 8 horas
c) 7 horas e meia
d) 7 horas e 15 minutos
e) 7 horas
Tentei o produto pela soma e não deu certo: chamando uma de A e outra de B, fiz o seguinte: A=4 horas
não consigo usar as fórmulas.
-
clovis22
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Jan 14, 2011 14:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: LETRAS
- Andamento: formado
 por Pedro123 » Sex Jan 14, 2011 17:03
por Pedro123 » Sex Jan 14, 2011 17:03
Faça o seguinte, crie uma "formula" do tipo, Rendimento . tempo = n peças
e tente achar um em função do outro, fazendo isso achei 8 horas, está certo? abrass, se nao conseguir avise
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Elcioschin » Sex Jan 14, 2011 18:12
por Elcioschin » Sex Jan 14, 2011 18:12
2 h 40 min = 2 h + 2/3 h = 8/3 h
1/(8/3) = 1/4 + 1/T
1/T = 3/8 - 1/4
1/T = 1/8
T = 8 horas
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por clovis22 » Sáb Jan 15, 2011 08:01
por clovis22 » Sáb Jan 15, 2011 08:01
Eu agradeço aos dois pela resolução e a resposta é essa mesma. Muito obrigado. Embora eu tenha me formado em Letras, adoro Matemática e sempre que posso, procuro praticar. Gosto muito de geometria espacial, porém não me sobra tempo para estudar, pois este ano farei Ciências Contábeis, visando concurso para Fiscal.
-
clovis22
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Jan 14, 2011 14:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: LETRAS
- Andamento: formado
 por clovis22 » Sáb Jan 15, 2011 08:09
por clovis22 » Sáb Jan 15, 2011 08:09
-
clovis22
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Jan 14, 2011 14:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: LETRAS
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- matemática comercial
por clovis22 » Dom Jan 16, 2011 18:11
- 0 Respostas
- 1325 Exibições
- Última mensagem por clovis22

Dom Jan 16, 2011 18:11
Álgebra Elementar
-
- Desconto comercial
por brunotst » Dom Out 31, 2010 13:25
- 1 Respostas
- 1692 Exibições
- Última mensagem por esteban

Dom Out 31, 2010 16:30
Matemática Financeira
-
- Desconto Comercial
por andreltr » Qui Jul 28, 2011 15:27
- 1 Respostas
- 1561 Exibições
- Última mensagem por Rogerio Murcila

Sex Jul 29, 2011 13:57
Matemática Financeira
-
- Desconto comercial simples
por Larice Mourao » Qua Nov 21, 2012 21:19
- 2 Respostas
- 5323 Exibições
- Última mensagem por Larice Mourao

Qui Nov 22, 2012 13:32
Matemática Financeira
-
- Juros Simples EXATO e COMERCIAL
por sempre_aprendendo » Qui Ago 18, 2011 11:14
- 1 Respostas
- 6601 Exibições
- Última mensagem por Caradoc

Sex Ago 19, 2011 13:47
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




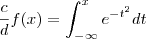

 .
.



