Encontre todos os pares de inteiros positivos
 tais que
tais que 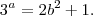
Já tentei fazer por congruência modular, não deu certo..
alguém tem alguma ideia?

 tais que
tais que 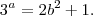

 ,perceba que se" b" for impar "a" é impar e se "b "for par "a" é par.
,perceba que se" b" for impar "a" é impar e se "b "for par "a" é par.![\left[ \sqrt[]{3}{(3)}^{n}-\sqrt[]{2}(2k+1)\right].\left[\sqrt[]{3}{(3)}^{n}+\sqrt[]{2}(2k+1) \right]=1 \left[ \sqrt[]{3}{(3)}^{n}-\sqrt[]{2}(2k+1)\right].\left[\sqrt[]{3}{(3)}^{n}+\sqrt[]{2}(2k+1) \right]=1](/latexrender/pictures/9e7beedbb70d3f969bdde73a596556d5.png) e como n e k são naturais essa equação é impossivel.
e como n e k são naturais essa equação é impossivel.![\left[{(3)}^{g}-\sqrt[]{2}(2r)\right].\left[{(3)}^{g}+\sqrt[]{2}(2r) \right]=1 \left[{(3)}^{g}-\sqrt[]{2}(2r)\right].\left[{(3)}^{g}+\sqrt[]{2}(2r) \right]=1](/latexrender/pictures/4cb7d25d03dd7bddf782a280b40af6ed.png) que por acaso a unica solução é a trivial.
que por acaso a unica solução é a trivial.
 , temos:
, temos:
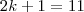 (visto que k deve ser positivo) e
(visto que k deve ser positivo) e  e
e  .
.
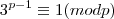 , como (p-1) é sempre par,para todo primo maior que 2, então "b=2k" mas o que é impossível dado que para
, como (p-1) é sempre par,para todo primo maior que 2, então "b=2k" mas o que é impossível dado que para 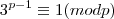 b=p. Tornando assim impossível "b" par ,para todo a=(p-1) maior do que 2.
b=p. Tornando assim impossível "b" par ,para todo a=(p-1) maior do que 2.
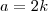 , assim
, assim  .
.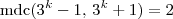 , então um fator 2 de um cancela o 2 em 2b^2, como nenhnum outro fator divide ambos os termos, teremos que um deles é um quadrado par, já que um deles é divisível por dois, e o outro por 4, e nenhum quadrado par pode ser incongruente a 4
, então um fator 2 de um cancela o 2 em 2b^2, como nenhnum outro fator divide ambos os termos, teremos que um deles é um quadrado par, já que um deles é divisível por dois, e o outro por 4, e nenhum quadrado par pode ser incongruente a 4 então uam solução é (2,2), pois como 3 é primo ele não pode ser decomposto em dois fatores distintos c-1 e c+1, logo o menor é igual a 1
então uam solução é (2,2), pois como 3 é primo ele não pode ser decomposto em dois fatores distintos c-1 e c+1, logo o menor é igual a 1 , mas
, mas 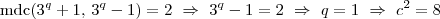 , impossível para c inteiro, veja que k deve ser par pois
, impossível para c inteiro, veja que k deve ser par pois  se e somente se 3^k é da forma 4n+1, pois se k for ímpar 3^k será a forma 4n+3, e 4n+3-1 não é divisível por 4
se e somente se 3^k é da forma 4n+1, pois se k for ímpar 3^k será a forma 4n+3, e 4n+3-1 não é divisível por 4 , então
, então 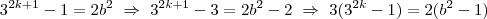

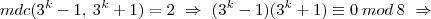 b é ímpar
b é ímpar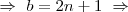
![b^2 = 4n(n+1)+1 \ \Rightarrow \ \: 3^{2k+1} - 1 = 2[4n(n+1)+1] \ \Rightarrow \ \: 3^{2k+1} = 8n(n+1)+3 \ \Rightarrow b^2 = 4n(n+1)+1 \ \Rightarrow \ \: 3^{2k+1} - 1 = 2[4n(n+1)+1] \ \Rightarrow \ \: 3^{2k+1} = 8n(n+1)+3 \ \Rightarrow](/latexrender/pictures/e16d97e133adbdd903ae9adeae70c83b.png)
 já que
já que  é um quadrado perfeito ímpar, ele deve ser da forma
é um quadrado perfeito ímpar, ele deve ser da forma 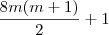 , logo
, logo
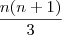 deve ser triangular, já que
deve ser triangular, já que  é triangular
é triangular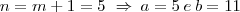
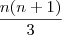 seja triangular e
seja triangular e  seja uma potência de 3.
seja uma potência de 3.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.