Como o material de que são feitas as condutas não é susceptível de ser dobrado, o tubo tem de ser cortado em dois sítios. Qual o ângulo de corte
?Repara que, dividindo o tubo por um corte, segundo um ângulo
, e rodando uma das partes 180º , é possível reajustar as secções. 
Este é o enunciado.
Eu comecei por determinar
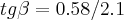e determinei a amplitude do ângulo 
, mas depois não estou a perceber como hei de acabar o exercício. PS: o resultado dá
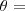82,28ºSe alguém me puder ajudar agradecia imenso.
por 
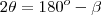
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.