eis a questao
![tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2}) tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2})](/latexrender/pictures/0b8089e9f8a70b48af87fd28e0028da8.png)
O problema é que para resolver tive que usar
![tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6} tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6}](/latexrender/pictures/891a35c858a89a573a619aabd8463ae8.png) e analogamente para o arco seno, desta forma obtive tg(5.30 - 60/4) e assim consegui chegar na resposta correta q é -1.
e analogamente para o arco seno, desta forma obtive tg(5.30 - 60/4) e assim consegui chegar na resposta correta q é -1.Porem não consegui resolver da mesma forma que y=cos(arsen(1/3)) onde
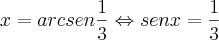 e depois pela relação fundametal obtendo o resultado
e depois pela relação fundametal obtendo o resultado ![y=\frac{2\sqrt[]{2}}{3} y=\frac{2\sqrt[]{2}}{3}](/latexrender/pictures/7f8f2b970ba46579aa392476a200a364.png) .
.Peço que me ajudem a resolver desta segunda maneira pois acabei chegando em tg5x...ai não da né..
desde ja agradeço, abs Henrique
"Ninguém é tão grande que não possa apender..nem tão pequeno que não possa ensinar"


![\alpha = arctg\frac{\sqrt[2]{3}}{3} \alpha = arctg\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/76fceb8f5724fb3f67a45c3f3975ef48.png)
![\beta = arcsen\frac{\sqrt[2]{3}}{2} \beta = arcsen\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/9aa38933a9c2222b6d4850f1ed213acd.png)
 e o
e o  pela tabela de sen,cos e tg.
pela tabela de sen,cos e tg.

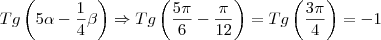

 e
e  . Vamos ver sem os valores de a e b:
. Vamos ver sem os valores de a e b:


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.