 por henrique_mat » Seg Ago 23, 2010 18:57
por henrique_mat » Seg Ago 23, 2010 18:57
Ola, sou novo aqui e na profissao de professor.
eis a questao
![tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2}) tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2})](/latexrender/pictures/0b8089e9f8a70b48af87fd28e0028da8.png)
O problema é que para resolver tive que usar
![tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6} tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6}](/latexrender/pictures/891a35c858a89a573a619aabd8463ae8.png)
e analogamente para o arco seno, desta forma obtive tg(5.30 - 60/4) e assim consegui chegar na resposta correta q é
-1.
Porem não consegui resolver da mesma forma que y=cos(arsen(1/3)) onde
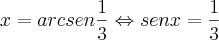
e depois pela relação fundametal obtendo o resultado
![y=\frac{2\sqrt[]{2}}{3} y=\frac{2\sqrt[]{2}}{3}](/latexrender/pictures/7f8f2b970ba46579aa392476a200a364.png)
.
Peço que me ajudem a resolver desta segunda maneira pois acabei chegando em tg5x...ai não da né..
desde ja agradeço, abs Henrique
"Ninguém é tão grande que não possa apender..nem tão pequeno que não possa ensinar"
-
henrique_mat
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Ago 23, 2010 18:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. matematica
- Andamento: formado
 por VtinxD » Seg Ago 23, 2010 20:16
por VtinxD » Seg Ago 23, 2010 20:16
Primeiro vamos nomear as coisas:
![\alpha = arctg\frac{\sqrt[2]{3}}{3} \alpha = arctg\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/76fceb8f5724fb3f67a45c3f3975ef48.png)
![\beta = arcsen\frac{\sqrt[2]{3}}{2} \beta = arcsen\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/9aa38933a9c2222b6d4850f1ed213acd.png)
Nós podemos achar o

e o

pela tabela de sen,cos e tg.
Pela tabela:


Agora subistuindo os valores na primeira equação:
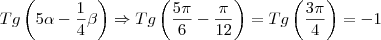
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por henrique_mat » Ter Ago 24, 2010 17:07
por henrique_mat » Ter Ago 24, 2010 17:07
Obrigado VtinxD , mas por este caminho eu ja consegui..o problema é resolver pelo mesmo caminho que esta resolvido o cos(arcsen)...abs
-
henrique_mat
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Ago 23, 2010 18:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. matematica
- Andamento: formado
 por MarceloFantini » Ter Ago 24, 2010 20:01
por MarceloFantini » Ter Ago 24, 2010 20:01
Mas você usou, a diferença é que os arcos eram conhecidos. Veja:

e

. Vamos ver sem os valores de a e b:

Não tem como resolver sem conhecer os valores.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por henrique_mat » Ter Ago 24, 2010 20:59
por henrique_mat » Ter Ago 24, 2010 20:59
Obrigado Fantini..acho q oq eu precisava era confirmar que esta questao nao da para ser resolvida sem conhecer os arcos, tenho outros exercicios como esse e agora tenho ctz q sem conhecer os arcos é impossivel...
Gostei do seu curso, adoraria fazer, mas por aqui nao tem..abs
-
henrique_mat
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Ago 23, 2010 18:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. matematica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [funções inversas]
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
- 2 Respostas
- 1735 Exibições
- Última mensagem por Ana_Rodrigues

Ter Jan 24, 2012 22:33
Funções
-
- funções inversas
por Edgard Guarido » Sex Mar 07, 2014 18:53
- 2 Respostas
- 2602 Exibições
- Última mensagem por Edgard Guarido

Qui Mar 13, 2014 15:54
Funções
-
- Funções circulares inversas
por Ananda » Qui Mar 20, 2008 20:03
- 2 Respostas
- 4802 Exibições
- Última mensagem por Ananda

Seg Mar 24, 2008 17:13
Trigonometria
-
- funçoes circulares inversas
por Thassya » Sex Mai 29, 2009 11:29
- 3 Respostas
- 2521 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 10:18
Trigonometria
-
- Função Circulares inversas 2
por Fernanda90 » Qui Ago 27, 2009 16:52
- 2 Respostas
- 4223 Exibições
- Última mensagem por Fernanda90

Qui Ago 27, 2009 20:25
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2}) tg(5arctg\frac{\sqrt[]{3}}{3}-\frac{1}{4}arcsen\frac{\sqrt[]{3}}{2})](/latexrender/pictures/0b8089e9f8a70b48af87fd28e0028da8.png)
![tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6} tga=\frac{\sqrt[]{3}}{3}\Rightarrow a=\frac{\pi}{6}](/latexrender/pictures/891a35c858a89a573a619aabd8463ae8.png) e analogamente para o arco seno, desta forma obtive tg(5.30 - 60/4) e assim consegui chegar na resposta correta q é -1.
e analogamente para o arco seno, desta forma obtive tg(5.30 - 60/4) e assim consegui chegar na resposta correta q é -1.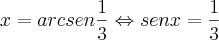 e depois pela relação fundametal obtendo o resultado
e depois pela relação fundametal obtendo o resultado ![y=\frac{2\sqrt[]{2}}{3} y=\frac{2\sqrt[]{2}}{3}](/latexrender/pictures/7f8f2b970ba46579aa392476a200a364.png) .
.

![\alpha = arctg\frac{\sqrt[2]{3}}{3} \alpha = arctg\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/76fceb8f5724fb3f67a45c3f3975ef48.png)
![\beta = arcsen\frac{\sqrt[2]{3}}{2} \beta = arcsen\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/9aa38933a9c2222b6d4850f1ed213acd.png)
 e o
e o  pela tabela de sen,cos e tg.
pela tabela de sen,cos e tg.

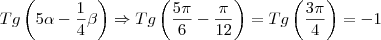

 e
e  . Vamos ver sem os valores de a e b:
. Vamos ver sem os valores de a e b:




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.