não entendi o gabarito oficial , a resposta é muito suprimida , encurtada , não gostei e não entendi o desenvolvimento .
vamos a questão :
Um capital é aplicado por doze anos e seis meses a juros compostos de meio por cento ao mês .
Ao final desse período , o rendimento acumulado será igual , inferior ou superior a 100 % ?
Justtifique sua resposta


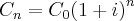

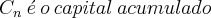

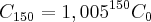
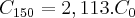
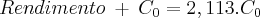




 .
.



