Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por minyamasaki » Ter Jun 01, 2010 17:58
por minyamasaki » Ter Jun 01, 2010 17:58
Quero colocar a inequação |x|<a da seguinte forma:
(i) Se |x|<a então multiplicando os dois membros da inequação por 1/(a*|x|) temos que (1/a)<(1/|x|) considerando que x seja um numero negativo, pela definição de modulo, temos então que (1/a)<(-1/x).
(ii) Se |x|<a, considerando que x seja um número negativo logo, -x<a multiplicando os dois menbros da inequação por -1 temos que x>-a multiplicando novamente os dois membros por 1/(a*x) temos que (1/a)>(-1/x).
Porque os resultados de (i) e (ii) são diferentes e qual seria a resposta correta ?
-
minyamasaki
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jun 01, 2010 17:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por MarceloFantini » Ter Jun 08, 2010 19:00
por MarceloFantini » Ter Jun 08, 2010 19:00
Você errou na parte (ii). Na primeira, lembre-se que você multiplicou por

. Ou seja, se x é negativo, retirando o módulo teria que multiplicar por

, o que você
não fez na segunda parte, e simplesmente assumiu que x era positivo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jce_335 » Dom Ago 08, 2010 18:04
por jce_335 » Dom Ago 08, 2010 18:04
Você errou em

quando multiplicou

por
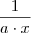
. Isso não implica em

, como você disse. Na verdade aquilo equivale a

, pois você mutiplicou a desigualdade por um número negativo:
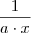
.
Note que

é positivo, pois você afirmou que

e o módulo de um número é sempre positivo ou nulo. Por conveniência você afirmou
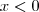
, logo a expressão
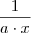
é negativa.
-
jce_335
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 23, 2010 13:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- N entendi a resolucao, questao de g p, alguem pode explicar?
por bmachado » Ter Mar 27, 2012 00:32
- 1 Respostas
- 4037 Exibições
- Última mensagem por bmachado

Ter Mar 27, 2012 22:35
Geometria Plana
-
- Alguém pode responder e me explicar essas questões?
por Blackhawk » Sex Mai 30, 2014 00:49
- 0 Respostas
- 1227 Exibições
- Última mensagem por Blackhawk

Sex Mai 30, 2014 00:49
Geometria Plana
-
- Alguém poderia me explicar passo a passo?
por arthurvct » Dom Abr 21, 2013 17:12
- 1 Respostas
- 1476 Exibições
- Última mensagem por ant_dii

Seg Abr 22, 2013 00:31
Cálculo: Limites, Derivadas e Integrais
-
- Me ajudem!!! Função para explicar!!!
por paulag » Qui Nov 11, 2010 07:44
- 0 Respostas
- 827 Exibições
- Última mensagem por paulag

Qui Nov 11, 2010 07:44
Funções
-
- Podem me explicar essa equação -> a/b = a * (1/b)
por osdeving » Qua Fev 12, 2014 20:14
- 1 Respostas
- 1218 Exibições
- Última mensagem por osdeving

Qua Fev 12, 2014 23:29
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Ou seja, se x é negativo, retirando o módulo teria que multiplicar por
. Ou seja, se x é negativo, retirando o módulo teria que multiplicar por  , o que você
, o que você 

 quando multiplicou
quando multiplicou  por
por 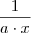 . Isso não implica em
. Isso não implica em  , como você disse. Na verdade aquilo equivale a
, como você disse. Na verdade aquilo equivale a  , pois você mutiplicou a desigualdade por um número negativo:
, pois você mutiplicou a desigualdade por um número negativo:  é positivo, pois você afirmou que
é positivo, pois você afirmou que  e o módulo de um número é sempre positivo ou nulo. Por conveniência você afirmou
e o módulo de um número é sempre positivo ou nulo. Por conveniência você afirmou 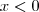 , logo a expressão
, logo a expressão 
 .
.



