 por Alessandrasouza » Sex Mai 14, 2010 15:44
por Alessandrasouza » Sex Mai 14, 2010 15:44
Olá tenho um problema que está me fazendo quebrar a cabeça e ñ consigo resolvê-lo de modo algum. É assim:
O segundo termo de uma PA é 15 e o a5=21. Calcular a soma dos 10 termos.
Eu tentei encontar o a1 da seguinte forma: 21=a1=(15-1).r
a1= 21-14
a1= 7ñ sei se, de fato, consegui encontrar o a1 e tbm ñ faço ideia de como tentar encontrar a razão

Por favor se alguém puder me ajudar, obrigada. Tenho q entregar na próxima segunda, dia 17/05/10..
Atenciosamente,
Alessandra
-
Alessandrasouza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mai 14, 2010 15:10
- Formação Escolar: EJA
- Área/Curso: ensino médio
- Andamento: cursando
 por Cleyson007 » Sex Mai 14, 2010 15:57
por Cleyson007 » Sex Mai 14, 2010 15:57
Boa tarde Alessandra!
Seja bem vinda ao Ajuda Matemática!
Alessandra, segue resolução:
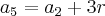
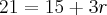

Procurando o primeiro termo:

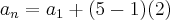
Resolvendo

Jogando na soma da P.A:
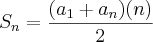
Resolvendo,

Comente qualquer dúvida,

Bons estudos!!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Alessandrasouza » Sex Mai 14, 2010 20:30
por Alessandrasouza » Sex Mai 14, 2010 20:30
Oi Cleyson,
obrigada pelas boas vindas e por ter respondido tão rapidamente...
sua resposta me ajudou bastante, tanto q verifiquei sozinha e consegui entender o a1.
Porém, estou com dúvida em relação a como vc conseguiu chegar no S=35
Antes eu calculei o número geral dos termos, de modo que:
an=a1+(n-1).r
a10=13+(10-1).2
a10=13+9.2
a10=31Jogando na soma da P.A., ficou:
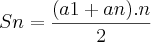
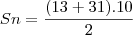 Sn=44.5
Sn=44.5
Sn=220 desse modo, meu Sn deu 220 ao invés de 35 como vc escreveu...
Gostaria de saber no q estou errando, se possível passo-a-passo...
Desde já agradeço, boa noite
Alessandra
-
Alessandrasouza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mai 14, 2010 15:10
- Formação Escolar: EJA
- Área/Curso: ensino médio
- Andamento: cursando
 por Cleyson007 » Sáb Mai 15, 2010 10:41
por Cleyson007 » Sáb Mai 15, 2010 10:41
Bom dia Alessandra!
Alessandra, fiz confusão (desculpe minha falta de atenção)

Achei o valor correspondente a soma dos cinco primeiros termos.. o problema pede a soma dos dez primeiros termos..
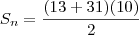
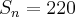
Sua resolução está correta sim!
Bons estudos!!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 07, 2012 01:13
- 2 Respostas
- 1309 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 07, 2012 01:31
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Dom Abr 08, 2012 21:10
- 2 Respostas
- 1631 Exibições
- Última mensagem por Anderson Alves

Qui Abr 12, 2012 22:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 14, 2012 13:42
- 1 Respostas
- 1666 Exibições
- Última mensagem por Lucio Carvalho

Sáb Abr 14, 2012 16:46
Progressões
-
- Progressões Aritméticas
por MarinaM » Dom Abr 15, 2012 00:24
- 2 Respostas
- 1827 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 19:56
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Ter Abr 17, 2012 22:30
- 3 Respostas
- 1997 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 21:46
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



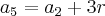
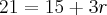


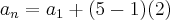

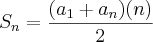




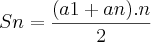
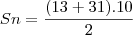

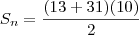
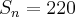
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.