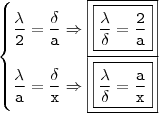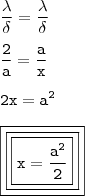Gabarito :

Minha tentativa:
Considerando
b é onde r corta y
c é onde s corta y
d é onde u corta y
e é onde v corta y
Sendo m coeficiente angular das retas r e s
é chamando m' de coeficiente angular de u e v
m=-b/a b=-am
m= -c/2 c=-2m
m'=-d/x d=-xm'
m'=-e/a e=-am'
Ao fazer as equações da reta, [b=-am, c= -2m, d= -xm e e=-am], cheguei em :
x+(-am)
r = xm-am
Seguindo a lógica:
s= xm-2m
u = xm-xm
v = xm-am
Encontrei P=m(-2+a) e Q=m(x-a)
Travei aqui, além disso, suponho que esteja errado.
Alguém pode me ajudar?


 e
e  , possivelmente, poderá obter a resposta utilizando os conceitos envolvendo
, possivelmente, poderá obter a resposta utilizando os conceitos envolvendo 
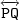 que passa pela origem. Por conseguinte, sejam
que passa pela origem. Por conseguinte, sejam 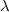 e
e 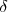 as distâncias dos pontos
as distâncias dos pontos  e
e 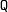 ao eixo
ao eixo  , respectivamente. Isto posto, temos que
, respectivamente. Isto posto, temos que 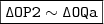 .
.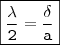 e
e  . Com efeito,
. Com efeito,