 por AnaFurtado » Sáb Mar 20, 2010 17:24
por AnaFurtado » Sáb Mar 20, 2010 17:24
Dados os pontos A(6) e B(-2), determine:
a) os simétricos dos pontos A e B em relação à origem
- Esse eu acredito que entendi, a simetria do número é o seu inverso né? O inverso de A fica -6 e de B fica 2.
b) a abscissa do ponto A', simétrico de A em relação a B
Fiquei em duvida, eu tentei resolver de 2 formas:
- d(A',B) = x(b) - x(a') = -2 - (-6) = 4
ou
- (A',B) = -6 -2 = 8
c) a abscissa do ponto B', simétrico de B em relação a A
Neste, a mesma história da B:
- d(B',A) = X(a) - X(b) = 6-2 = 4
ou
- (B',A) = 2 - 6 = -4
-
AnaFurtado
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mar 20, 2010 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Mar 22, 2010 23:36
por Molina » Seg Mar 22, 2010 23:36
Boa noite, Ana.
AnaFurtado escreveu:a) os simétricos dos pontos A e B em relação à origem
- Esse eu acredito que entendi, a simetria do número é o seu inverso né? O inverso de A fica -6 e de B fica 2.

AnaFurtado escreveu:b) a abscissa do ponto A', simétrico de A em relação a B

AnaFurtado escreveu:c) a abscissa do ponto B', simétrico de B em relação a A

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por alinter » Qua Mar 16, 2011 11:45
por alinter » Qua Mar 16, 2011 11:45
Segundo o Livro
Matemática Compelta - Giovanni e BonjornoRespostas:
a) A(-6); B(2)
b) A'(-10)
c) B'(14)
Resolução:
Simétrico em geometria geralmente quer dizer "A mesma distância, na mesma direção mas em sentido oposto."
A) "- Esse eu acredito que entendi, a simetria do número é o seu inverso né? O inverso de A fica -6 e de B fica 2."

B) A distância de A até B = |- 2 - 6|=> |- 8|=> 8 . Sendo 8 a distância entre os dois pontos(A,B), a distância de 8 apartir de B no sentido negativo(onde o sentido positivo já é 6(A)) será (- 2 - 8)= -10
A' = -10C) A distância de 8 no sentido positivo(onde o sentido negativo já é -2(B)) a partir de A temos: (6 + 8) = 14
B' = 14
-
alinter
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mar 16, 2011 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Mar 16, 2011 12:02
por LuizAquino » Qua Mar 16, 2011 12:02
AnaFurtado escreveu:Dados os pontos A(6) e B(-2), determine:
a) os simétricos dos pontos A e B em relação à origem
- Esse eu acredito que entendi, a simetria do número é o seu inverso né? O inverso de A fica -6 e de B fica 2.
Usualmente, o "simétrico" de um número real
a é o número
-a de tal modo que
a+(-a)=0.
Por outro lado, o "inverso" de um número real
a é o número

de tal modo que
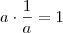
. Note que o 0 não possui inverso.
Exemplo: Dado o número 2, nós temos que:
- Simétrico: -2
- Inverso:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria espacial] Centros de simetria
 por rochadapesada » Seg Abr 08, 2013 21:57
por rochadapesada » Seg Abr 08, 2013 21:57
- 2 Respostas
- 2061 Exibições
- Última mensagem por rochadapesada

Qua Abr 10, 2013 16:15
Geometria Espacial
-
- [geometria analitica-vetores]alguém poderia resolver?
por amanda_k » Sáb Out 14, 2017 22:28
- 0 Respostas
- 4045 Exibições
- Última mensagem por amanda_k

Sáb Out 14, 2017 22:28
Geometria Analítica
-
- [geometria analitica-vetores]alguém poderia resolver?
por amanda_k » Sáb Out 14, 2017 22:31
- 0 Respostas
- 4075 Exibições
- Última mensagem por amanda_k

Sáb Out 14, 2017 22:31
Geometria Analítica
-
- [geometria analitica-vetores]alguém poderia resolver?
por amanda_k » Sáb Out 14, 2017 22:51
- 0 Respostas
- 4364 Exibições
- Última mensagem por amanda_k

Sáb Out 14, 2017 22:51
Geometria Analítica
-
- [Cálculo] Como resolver essa equação?
por martistapvai » Sex Out 14, 2011 10:18
- 0 Respostas
- 1211 Exibições
- Última mensagem por martistapvai

Sex Out 14, 2011 10:18
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




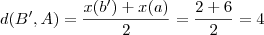

 de tal modo que
de tal modo que 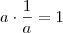 . Note que o 0 não possui inverso.
. Note que o 0 não possui inverso.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
