Dados os pontos A(6) e B(-2), determine:
a) os simétricos dos pontos A e B em relação à origem
- Esse eu acredito que entendi, a simetria do número é o seu inverso né? O inverso de A fica -6 e de B fica 2.
b) a abscissa do ponto A', simétrico de A em relação a B
Fiquei em duvida, eu tentei resolver de 2 formas:
- d(A',B) = x(b) - x(a') = -2 - (-6) = 4
ou
- (A',B) = -6 -2 = 8
c) a abscissa do ponto B', simétrico de B em relação a A
Neste, a mesma história da B:
- d(B',A) = X(a) - X(b) = 6-2 = 4
ou
- (B',A) = 2 - 6 = -4




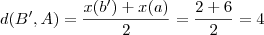

 de tal modo que
de tal modo que 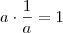 . Note que o 0 não possui inverso.
. Note que o 0 não possui inverso.

 .
.
 :
: