Olá Ananda, boa tarde!
Hoje pensei em um modo mais simples de fazer, sem argumentos do cálculo, utilizando o fato de o conjunto imagem da função seno ser limitado entre -1 e 1 e as definições da progressão geométrica, veja:
Nossa PG:
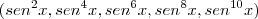
Com primeiro termo:

E razão:

Tal que
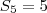
(soma dos 5 primeiros termos)
A conjunto imagem da função seno é limitado:

Como o quadrado de um número real nunca é negativo, segue que:

Considerando a razão que é

, vamos listar todas as possibilidades de classificação desta PG:
Caso I) Se

Implicaria uma PG constante com termos nulos.
Caso II) Se
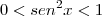
Implicaria uma PG decrescente com cada termo menor que o anterior.
Caso III) Se
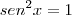
Implicaria uma PG constante com termos iguais e não nulos.
Agora, analisemos cada caso:
Caso I) Não convém, pois teríamos:
PG =

Com
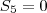
.
Caso II) Como
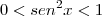
Segue que:
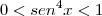
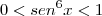

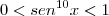
E então:


Que também não convém, pois teríamos:
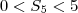 Caso III)
Caso III) É o caso restante.
Tanto que para
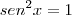
, vale a equação trigonométrica da soma de termos da PG:
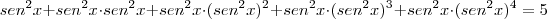
Logo, de fato,
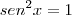
.
E segue que:

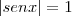
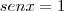
ou
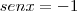
Portanto, o conjunto-solução é:
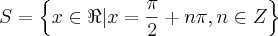
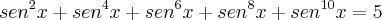 ?
?

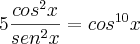




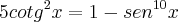

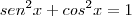

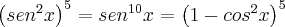

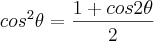

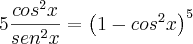
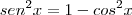



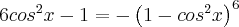
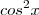 .
. :
:

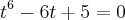



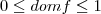

 (raiz no domínio)
(raiz no domínio)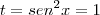

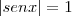


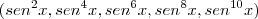
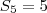 (soma dos 5 primeiros termos)
(soma dos 5 primeiros termos)
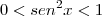
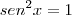

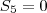 .
.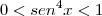
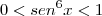

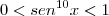


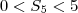
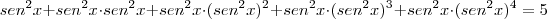
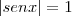
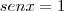 ou
ou 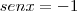
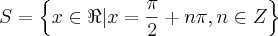

 .
.
 :
: