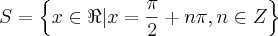-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Mar 10, 2008 02:30
por admin » Seg Mar 10, 2008 02:30
Olá Ananda!
Também há um outro colaborador pensando em sua dúvida.
Enquanto isso, verifique sua passagem.

Como exemplo da continuação da soma de termos, eu encontrei:
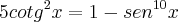
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Seg Mar 10, 2008 10:23
por Ananda » Seg Mar 10, 2008 10:23
Bom dia!
É diferente porque entra naquela resolução com binômio, né?
Vou tentar hoje resolver novamente para ver se enxergo algo novo!
Grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Mar 10, 2008 11:38
por admin » Seg Mar 10, 2008 11:38
Bom dia, Ananda.
Então, eu percebi que você considerou igual, mas a relação fundamental da trigonometria é:
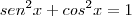
Esta igualdade é falsa:

Eu também já desenvolvi este binômio do terceiro membro, mas não obtive sucesso na simplificação da equação:
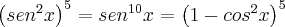
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Seg Mar 10, 2008 13:05
por admin » Seg Mar 10, 2008 13:05
Ananda, uma outra forma que pensei para lidar com este expoente 10, é utilizar esta redução de potência, seguida pela expansão binomial:

E quando as potências em cosseno aparecerem, utilizar esta outra redução:
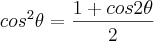
Pois

Mas este processo é desanimador, ainda prefiro tentar buscar um caminho melhor.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Seg Mar 10, 2008 13:42
por Ananda » Seg Mar 10, 2008 13:42
Se bem que na prova real não daria certo...
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Seg Mar 10, 2008 13:43
por Ananda » Seg Mar 10, 2008 13:43
Opa, dá sim!
Cos tem que ser zero, certo?
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Seg Mar 10, 2008 13:46
por Ananda » Seg Mar 10, 2008 13:46
Exatamente!
E eu me enrolei com a prova real e por fim, vi que estava dando:
0 = 1
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Seg Mar 10, 2008 13:55
por Ananda » Seg Mar 10, 2008 13:55
Partindo daí, só cheguei a:
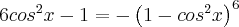
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Mar 10, 2008 14:09
por admin » Seg Mar 10, 2008 14:09
O que dá uma equação de grau 6 em
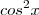
.
Mas, partindo de outro desenvolvimento, eu já tinha obtido outra equação de grau 6 em

:

Fazendo uma substituição:

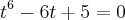
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Seg Mar 10, 2008 14:29
por Ananda » Seg Mar 10, 2008 14:29
E como se resolveria isso?
Em programa de função, acho a resposta, mas como se faz no lápis?
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Seg Mar 10, 2008 15:38
por Ananda » Seg Mar 10, 2008 15:38
Hmmm, grata...
De qualquer modo, a resolução desse exercício foi mais uma "curiosidade", já que não pretendo prestar ITA.
Mas conseguindo fazer todos ou quase todos os exercícios de cada capítulo, acredito que estarei mais apta a fazer as provas das faculdades que prestarei.
Mais uma vez, grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qua Mar 12, 2008 16:46
por admin » Qua Mar 12, 2008 16:46
Olá Ananda, boa tarde!
Hoje pensei em um modo mais simples de fazer, sem argumentos do cálculo, utilizando o fato de o conjunto imagem da função seno ser limitado entre -1 e 1 e as definições da progressão geométrica, veja:
Nossa PG:
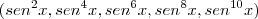
Com primeiro termo:

E razão:

Tal que
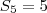
(soma dos 5 primeiros termos)
A conjunto imagem da função seno é limitado:

Como o quadrado de um número real nunca é negativo, segue que:

Considerando a razão que é

, vamos listar todas as possibilidades de classificação desta PG:
Caso I) Se

Implicaria uma PG constante com termos nulos.
Caso II) Se
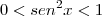
Implicaria uma PG decrescente com cada termo menor que o anterior.
Caso III) Se
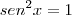
Implicaria uma PG constante com termos iguais e não nulos.
Agora, analisemos cada caso:
Caso I) Não convém, pois teríamos:
PG =

Com
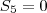
.
Caso II) Como
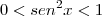
Segue que:
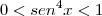
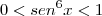

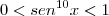
E então:


Que também não convém, pois teríamos:
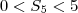 Caso III)
Caso III) É o caso restante.
Tanto que para
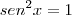
, vale a equação trigonométrica da soma de termos da PG:
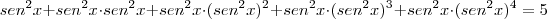
Logo, de fato,
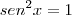
.
E segue que:

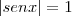
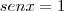
ou
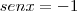
Portanto, o conjunto-solução é:
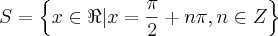
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Qui Mar 13, 2008 11:10
por Ananda » Qui Mar 13, 2008 11:10
Bom dia, Fábio!
Grata pela resolução mais prática!
Fico alegre de por enquanto estar sem novas dúvidas!
Grata mais uma vez!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4247 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4722 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4233 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2886 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
-
- Progressão Geométrica .-.
por Carolziiinhaaah » Seg Jun 14, 2010 13:56
- 3 Respostas
- 5918 Exibições
- Última mensagem por Carolziiinhaaah

Seg Jun 14, 2010 15:35
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
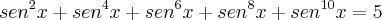 ?
?

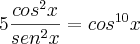




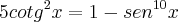

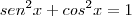

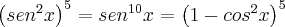

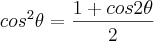

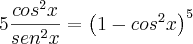
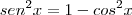



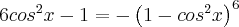
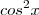 .
. :
:

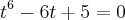



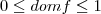

 (raiz no domínio)
(raiz no domínio)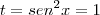

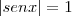


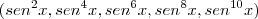
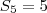 (soma dos 5 primeiros termos)
(soma dos 5 primeiros termos)
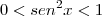
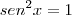

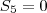 .
.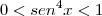
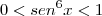

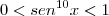


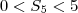
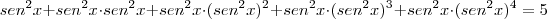
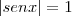
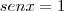 ou
ou