por rgladstone01 » Sáb Dez 13, 2014 00:11
O número - 19/38 é igual a:
a) 2 b) 1/2 c) 2 d) -1 e) - 1/2
Neste caso não consegui simplificar, verifiquei que os números são primo entre si, resposta d), porém o gabarito indicou e), por favor me ajudem.
-
rgladstone01
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sex Dez 12, 2014 23:59
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Redes de Computadores
- Andamento: formado
por nakagumahissao » Sáb Dez 13, 2014 11:25
rgladstone01,
Olha, para simplificar você deve pensar assim: "qual é o número que divide tanto o numerador quanto o denominador?". Neste caso, é o próprio 19. Assim:
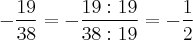
Resposta: Letra (e)
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário
-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Relação entre Conjuntos] Relações de Equivalência
por andrelangoni » Qui Abr 20, 2017 23:12
- 0 Respostas
- 2130 Exibições
- Última mensagem por andrelangoni
Qui Abr 20, 2017 23:12
Conjuntos
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 1972 Exibições
- Última mensagem por janderson77
Seg Dez 02, 2013 12:00
Trigonometria
-
- Equivalência
por Ivo Silva2014 » Dom Mar 23, 2014 16:38
- 0 Respostas
- 1037 Exibições
- Última mensagem por Ivo Silva2014
Dom Mar 23, 2014 16:38
Conjuntos
-
- RELAÇÃO DE EQUIVALENCIA
por EANDRIOLI » Seg Abr 23, 2012 01:51
- 0 Respostas
- 1174 Exibições
- Última mensagem por EANDRIOLI
Seg Abr 23, 2012 01:51
Álgebra Elementar
-
- Relação de Equivalência
por livia02 » Qui Ago 15, 2013 16:03
- 3 Respostas
- 2255 Exibições
- Última mensagem por MateusL
Sex Ago 23, 2013 15:50
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
