 por troziinho » Sex Nov 28, 2014 23:40
por troziinho » Sex Nov 28, 2014 23:40
Boa noite, estava tentando resolver este exercicio, porém me surgiu uma dúvida, sabemos que o cos(1/x) não existe quando x tende a zero, então como eu poderia fazer para tornar essa função continua no intervalo pedido? E quanto a derivabilidade?

-
troziinho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 28, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Prod
- Andamento: cursando
 por adauto martins » Dom Nov 30, 2014 11:43
por adauto martins » Dom Nov 30, 2014 11:43

,faz-se

...logo
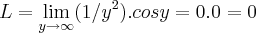
,entao
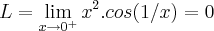
...
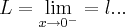
...logo nao existe o limite em 0 e a funçao nao e continua em 0...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4771 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade/Limites
 por joaofonseca » Sáb Dez 03, 2011 19:40
por joaofonseca » Sáb Dez 03, 2011 19:40
- 3 Respostas
- 2139 Exibições
- Última mensagem por LuizAquino

Sáb Dez 03, 2011 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Limites e continuidade
por Marcos_Mecatronica » Sáb Abr 27, 2013 19:38
- 2 Respostas
- 1723 Exibições
- Última mensagem por e8group

Dom Abr 28, 2013 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Limites(Continuidade)
 por brunotorres123-abc » Sáb Mar 21, 2015 19:35
por brunotorres123-abc » Sáb Mar 21, 2015 19:35
- 0 Respostas
- 1748 Exibições
- Última mensagem por brunotorres123-abc

Sáb Mar 21, 2015 19:35
Cálculo: Limites, Derivadas e Integrais
-
- Limites e Continuidade
por elisafrombrazil » Qui Jan 19, 2017 11:11
- 3 Respostas
- 5433 Exibições
- Última mensagem por adauto martins

Sex Jan 20, 2017 16:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 ,faz-se
,faz-se  ...logo
...logo 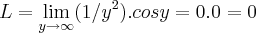 ,entao
,entao 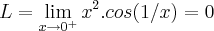 ...
...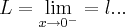 ...logo nao existe o limite em 0 e a funçao nao e continua em 0...
...logo nao existe o limite em 0 e a funçao nao e continua em 0...

 .
.



